The Lean Theorem Prover
Leonardo de Moura (Microsoft Research),
Gabriel Ebner (Vienna University of Technology),
Jared Roesch (University of Washington),
Sebastian Ullrich (Karlsruhe Institute of Technology)
POPL, Paris, 2017/01/16
http://leanprover.github.io/
http://leanprover.github.io/presentations/20170116_POPL
The Lean Theorem Prover Team
- The presenters, and
- Jeremy Avigad (CMU),
- Floris van Doorn (CMU),
- Rob Lewis (CMU),
- Daniel Selsam (Stanford)
Many thanks to
- Soonho Kong (former member)
- Jakob von Raumer (former member)
- Cody Roux
- Georges Gonthier
- Grant Passmore
- Nikhil Swamy
- Assia Mahboubi
- Bas Spitters
- Steve Awodey
- Ulrik Buchholtz
- Tom Ball
- Parikshit Khanna
- Haitao Zhang
Introduction: Lean
- New open source theorem prover
- Platform for
- Software verification & development
- Formalized mathematics
- Education (mathematics, logic, computer science)
- Synthesis (proofs & programs)
- de Bruijn's Principle: small trusted kernel
- Expressive logic
- Partial constructions: automation fills the "holes"
- Meta-programming
Introduction: Lean
Main Goal
Lean aims to bring two worlds together
- An interactive theorem prover with powerful automation
- An automated reasoning tool that
- produces (detailed) proofs,
- has a rich language,
- can be used interactively, and
- is built on a verified mathematical library
- A programming environment in which one can
- compute with objects with a precise formal semantics,
- reason about the results of computation, and
- write proof-producing automation
- It is an ongoing and long long term effort
What is new?
- Meta-programming
- Extend Lean using Lean
- Access Lean internals using Lean
- Proof/Program synthesis
- Powerful elaboration engine that can handle
- Higher-order unification
- Type classes
- Coercions
- Ad-hoc polymorphism (aka overloading)
"By relieving the brain of all unnecessary work, a good notation sets it free to concentrate on more advanced problems, and in effect increases the mental power of the race." – A. N. Whitehead
What is new?
- Small trusted kernel
- It does not contain
- Termination checker
- Fixpoint operators
- Pattern matching
- Module management
- It does not contain
- Reference type checker in Haskell
- Multi-core support
- Compile files in parallel
- Compile theorems in parallel
What is new?
- Simple json-based protocol for communicating with editors
- Fast incremental compilation
- Auto completion
- Type information
- Goal visualization
- We already support: Emacs, VS Code and ACE editor
- Profiler and Debugger for Lean code
- We can use them to profile/debug tactics since tactics are written in Lean.
What is new?
- Bytecode and C++ generator
- Many efficient native tactics implemented in C++
- Simplifier
- Congruence closure
- E-matching
- Ground AC completion
- (more coming soon)
Agenda
- Lean language
- Tactics and Meta-programming
- SMT-based tactics
- Superposition prover
- Profiler and Debugger
- Native code generator
The Logical Framework
- Dependent lambda calculus
The Logical Framework
The Logical Framework
- Hierarchy of universes
- Universe polymorphic definitions
Implicit arguments
The Logical Framework
- Chapter 7, Theorem Proving in Lean
Inductive families
inductive nat | zero : nat | succ : nat → nat inductive tree (α : Type u) | leaf : α → tree | node : tree → tree → tree inductive vector (α : Type) : nat → Type | nil : vector zero | cons : Π {n : nat}, α → vector n → vector (succ n)
Inductive families
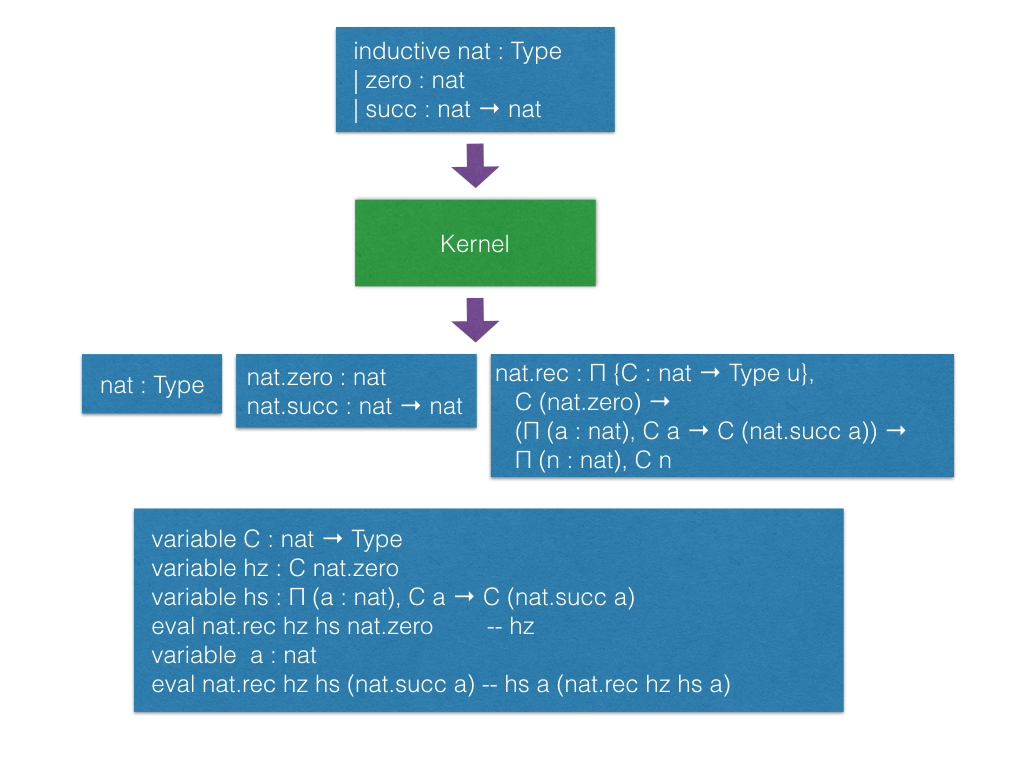
Recursive equations
- Chapter 8, Theorem Proving in Lean
- Recursors are inconvenient to use.
- Compiler from recursive equations to recursors.
- Two compilation strategies: structural and well-founded recursion
- Well-founded recursion is coming soon.
- Proofs by induction
Recursive equations
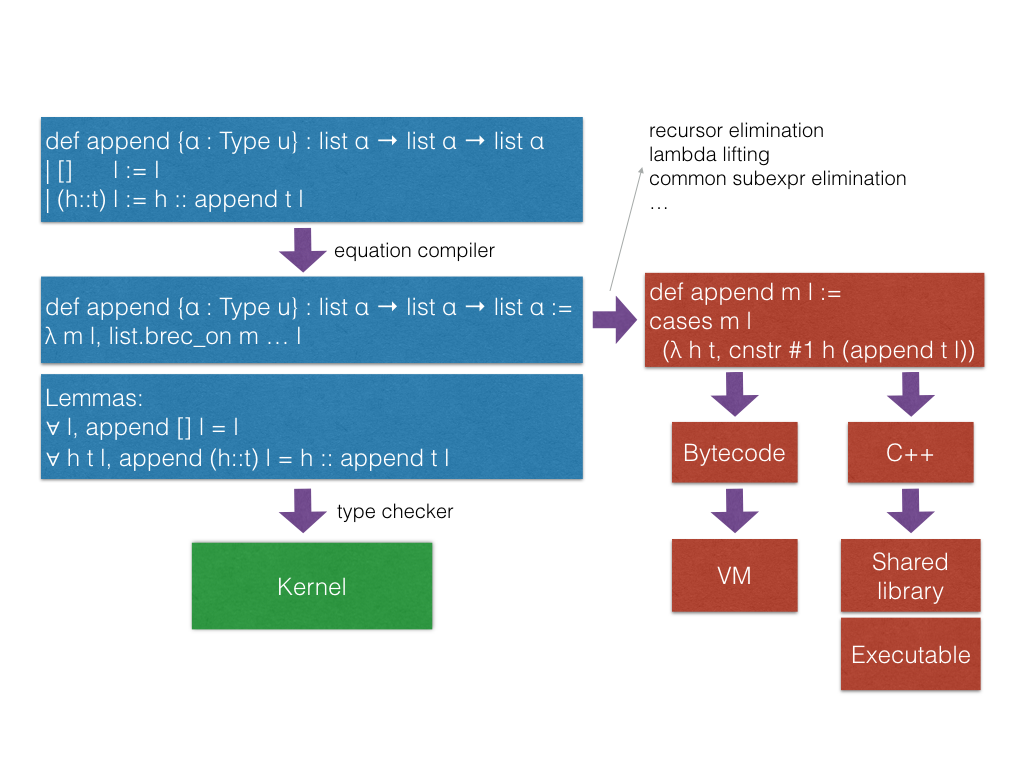
Recursive equations
- Dependent pattern matching
Structures
- Chapter 9, Theorem Proving in Lean
Type classes
- Chapter 10, Theorem Proving in Lean
Type classes
Coercions as type classes
- Chapter 10, Theorem Proving in Lean
Lean in Action
Meta-programming
- Extending Lean in Lean
Lean has an efficient bytecode interpreter
inductive expr | var : unsigned → expr | sort : level → expr | const : name → list level → expr | app : expr → expr → expr ... meta constant tactic_state : Type
Meta-programming
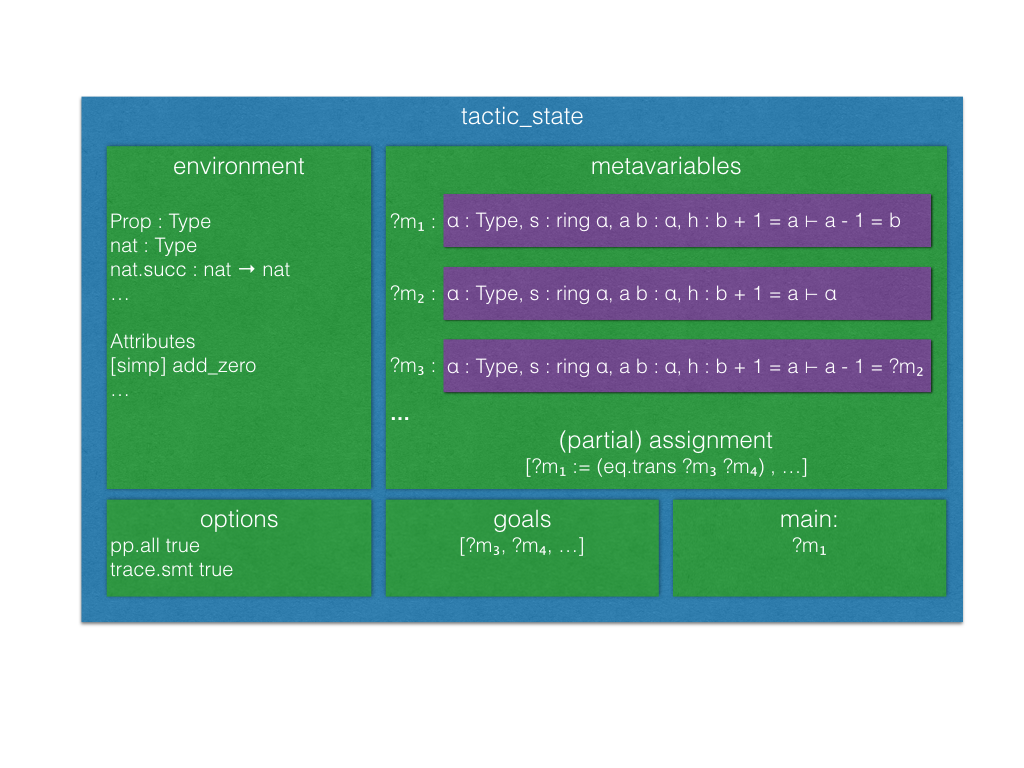
Meta-programming
Meta-programming
- The
by tacinstructs Lean to usetac : tactic unitto synthesize the missing term. - Demo
Meta-programming
Interactive mode
- Many users want to apply tactics interactively.
- They want to observe intermediate
tactic_state's. They want to avoid quotations, and gloss over the distinction between object and meta expressions.
-- They want to write exact eq.trans h₁ (eq.symm h₂) -- instead of to_expr `(eq.trans h₁ (eq.symm h₂)) >>= exact -- or the following, assuming (exact : pexpr -> tactic unit) exact `(eq.trans h₁ (eq.symm h₂)) - Lean provides an "interactive mode" for applying tactics.
- Demo
Backward Chaining
back.lean: simple Lean tactic for list membership goals using backward chaining.back_trace.lean: adds tracing to the previous tactic.back_inplace.lean: same example implemeted on top of theapplytactic.builtin.lean: same example using the builtin backward chaining tactic.ematch.lean: same example using heuristic instantiation. Actually, this one is not a form of backward chaining.- Later, we return to this example using the Lean superposition theorem prover.
Associative Commutative operators
builtin_ac.lean: Lean has builtin support for associative commutative operators, but this is not the point of this exercise.flat_assoc.lean: a tactic to "flatten" nested applications of associative operators. This tactic uses only basic primitives.flat_assoc_trace.lean: tracing tactic execution.ac_by_simp.lean: simplifier demo.
SMT tactic framework
- It implements gadgets found in state-of-the-art SMT solvers
- Congruence closure
- E-matching
- Unit propagation
- AC
- Arithmetic (coming soon)
smt_goalcontains the state of the SMT "gadgets" for a particular goal."Attaching more state to
tactic_state".meta constant smt_goal : Type meta def smt_state := list smt_goal meta def smt_tactic := state_t smt_state tactic - Users can solve problems interactively, and/or write their own "end game" tactics.
- We provide Lean APIs for traversing equivalence classes, inspecting instances and lemmas used for E-matching, etc.
Lifting tactic ==> smt_tactic
- Any
tacticthat does not change the set of hypotheses can be easily lifted because they do not invalidate thesmt_state. - Tactic
smt_tactic.intros- Add new hypothesis, and update
smt_state. - It will update equivalence classes, propagate equalities, etc.
- Add new hypothesis, and update
- Tactics that modify the set of hypotheses (e.g.,
revert,induction) can be lifted, but the affectedsmt_goal's are reconstructed from scratch.
SMT interactive mode
SMT tactic framework demo
Superposition prover
- Implemented 100% in Lean
- 2200 lines of code
- including toy SAT solver
- Uses Lean expressions, unification, proofs
- Complete for first-order logic with equality
- Similar to metis in Isabelle
Superposition prover
- Based on refutation of formulas in clause normal form (CNF)
- Applies inferences until contradiction (empty clause)
Superposition prover
- Inferences (modulo unification)
- and others
Superposition prover
- Gadgets
- Term ordering
- Selection
- Subsumption
- Demodulation
- Splitting
- "Best-effort" intuitionist proofs
- To be done:
- Term indexing
- AC redundancy elimination
Superposition prover
- State transformer of tactic monad
Superposition prover demos
- usage.lean: shows the basic usage of the super tactic
- clauses.lean: shows the data structure used for clauses
- assoc.lean: support for associative-commutative function symbols; as an example we show how to obtain the right inverse from the left inverse in monoids
- listex.lean: reasoning about membership in lists
- heapex.lean: proving a lemma about the disjoint union of heaps in separation logic, [that we proved before using E-matching](TODO)
Superposition prover
- Future work
- Performance
- Application of simplification rules
- Use of standard library
- Integration with SMT tactics
- Better clause representation
- Heterogeneous equality
- Configurability
- "Leanhammer"
Profiler
- Based on sampling
- It takes snapshots of the VM stack every x ms (default: 10 ms)
- Useful for finding performance bottlenecks in tactics
- Demo
Debugger
- We can monitor the VM execution.
Debugger
- Lean comes with a simple CLI debugger implemented in Lean on top of the VM monitor API.
Native Compiler
- Lean is able to compile your programs no configuration needed
lean --compile hello.lean ./hello "Hello Lean!"
- Goal is to produce efficient native code given a Lean term
- Assign computational intepretations to programs outside the logic (i.e
io) - Verify and execute programs without friction
Native Compiler Design
- Use C++ as a high level assembler, makes code generation, linking with runtime, and calling into the VM easy
- Current compiler is the third generation
- Initial prototype was implemented in C++
- How to increase:
- Confidence in correctness
- Ease of implementation
- Reusability
Self Hosting
- Application of a repeated theme: script Lean in Lean
- shares phases with VM compiler
- Transform higher order, dependently typed lambda
calculus to
ir:- an imperative language in A Normal Form.
- Denote IR into C++
- Easier to prototype and configure then LLVM
- Easily call runtime primitives
- Rely on standard C++ optimizations
- Enables verification of the compiler from
exprtoir
Self Hosting
- A fragment of the IR compiler written in Lean
able to use:
- Monad transformers
@[reducible] meta def ir_compiler (A : Type) := resultT (state ir_compiler_state) error A - Higher level operations, reduces boilerplate
present in C++ prototype (i.e
monad.map) - Reason and verify properties about the compiler
Compiler Design
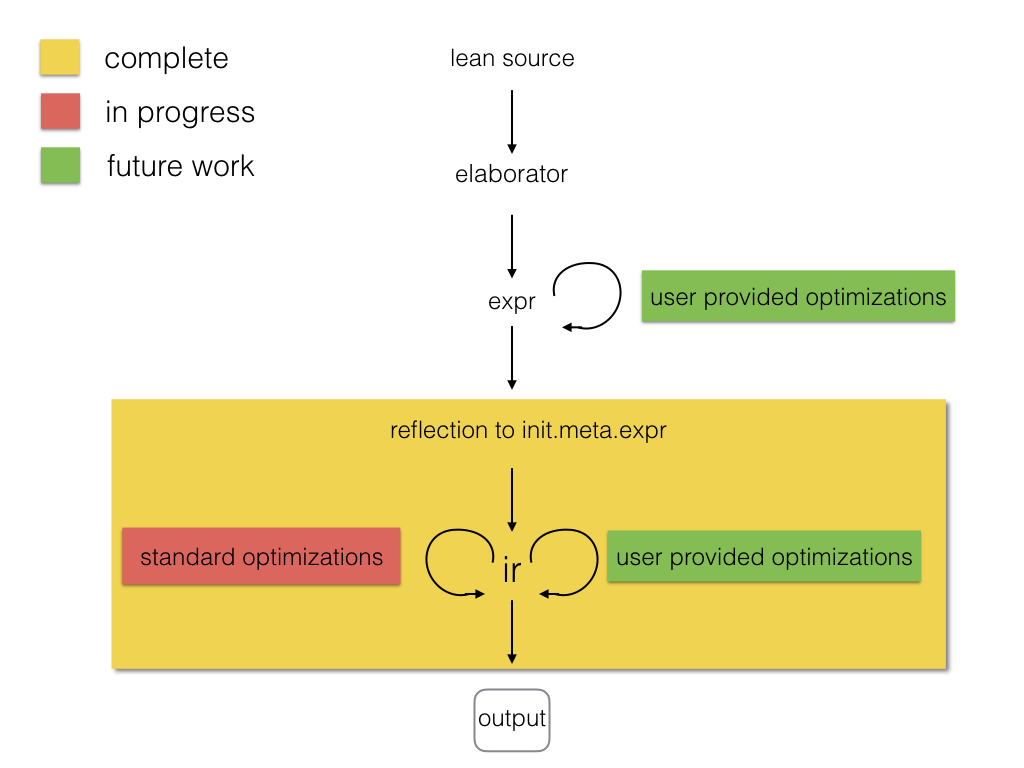
Efficient tactics
- Tactics written in Lean are accesible to average user
- Enables scripting low level automation
- Accelerate tactics using compilation, and optimization
- Build shared library per package; dynamically load at runtime
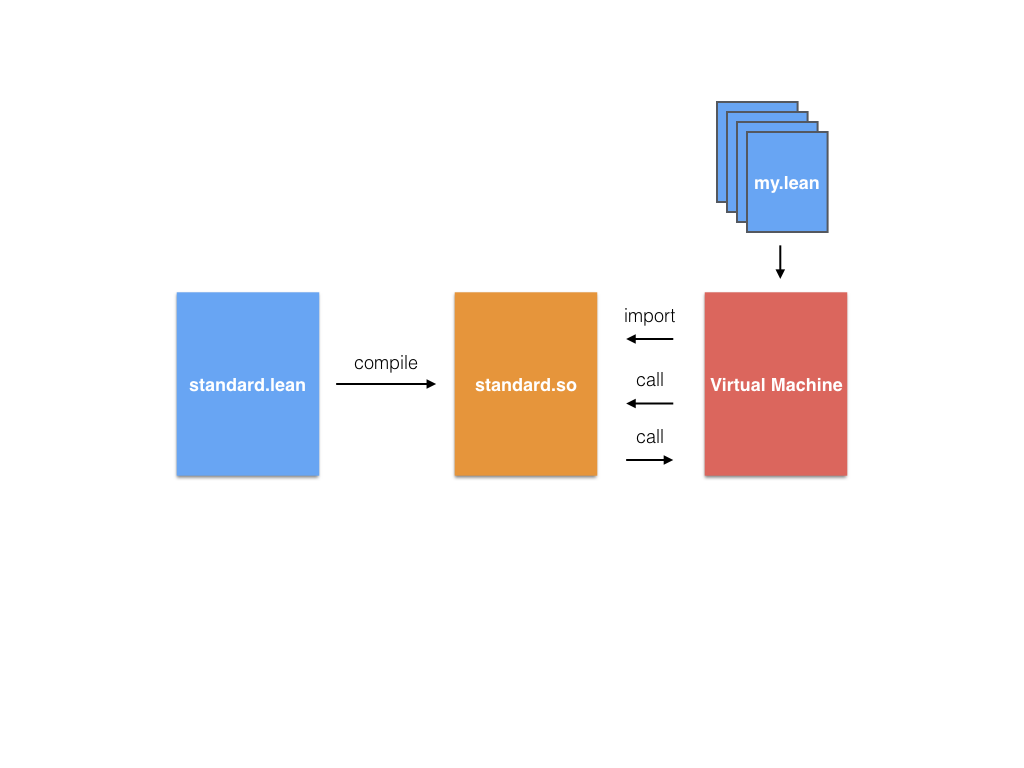
Programming
- Write a program, verify a property, compile and run
No need to configure; convention over configuration
lean --compile my_source_code.lean
- Configuration still exists.
- Future plans for user extension, philoshophy is well-designed libraries should package:
- Inductive types and their operations
- Lemmas about types and definitions in the library
- Tactics for reasoning about the library
- Refinements for executing the library efficiently
Work in progress
- Package level compilation
- Compile entire package into native code, which can be loaded by the VM
- Implemented but needs multi-platform support and polish
- Allow user provided IR refinements, with refinement proofs
- Basic support for replacing types + operations with implementations in IR
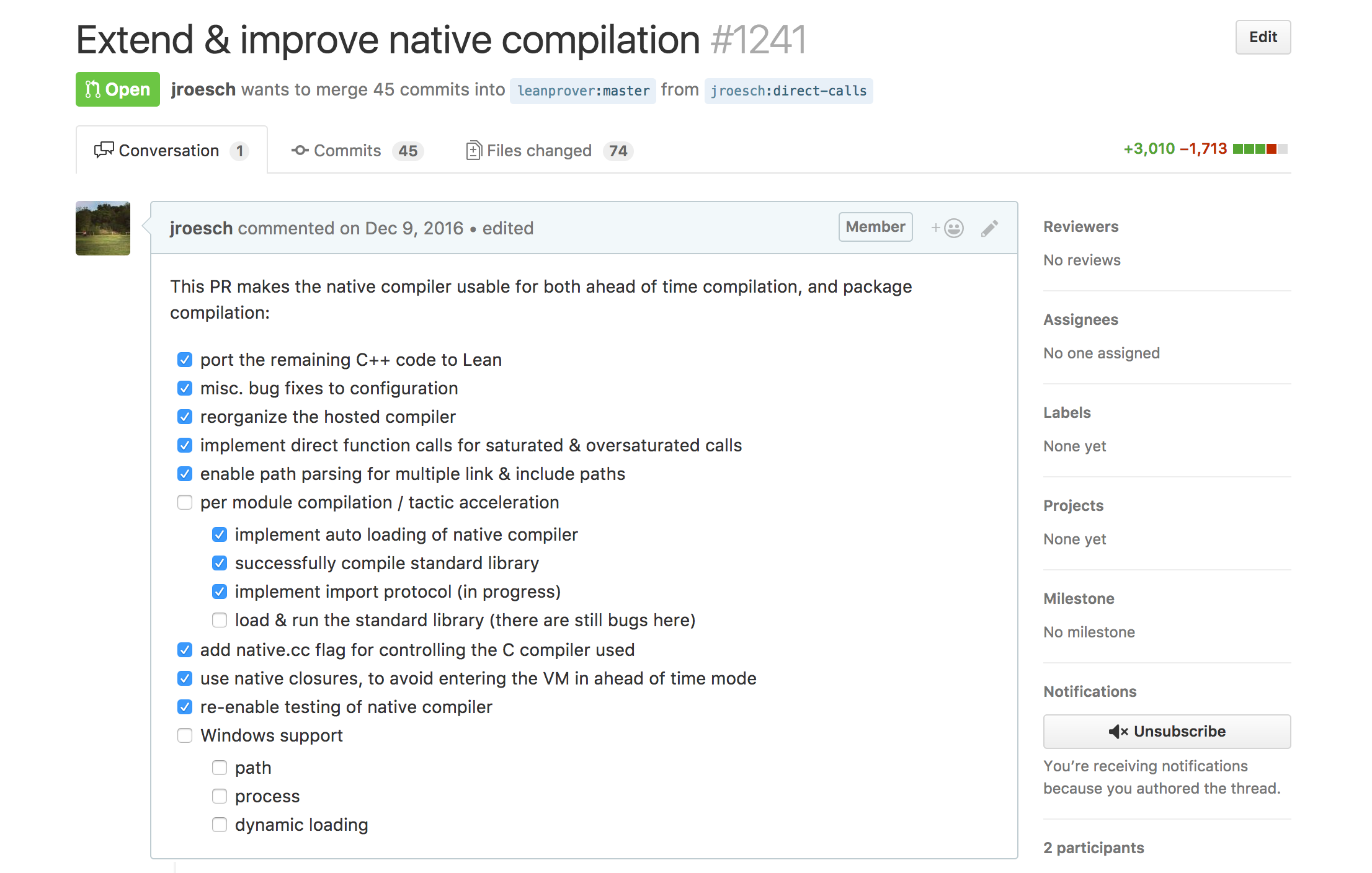
- The version of the native compiler in
masteris incomplete - The next iteration is nearing completion, and contains
many of the features discussed above.
- More details here: https://github.com/leanprover/lean/pull/1241
Work in progress
Future Work
- Framework for rewriting based on equality (in the theory, i.e
eqheq)- We can use exisiting simplifier as an optimizer
- Formally verifiy compiler
- Give formal semantics to all IRs
- Finish IR typechecker, and type system
- Apply traditional compiler verification techniques (CompCert, …)
Native Compiler Demo
- Configuring the native compiler
- Inspecting generated code
- Executing it in ahead of time mode
- More
Project suggestions
- Write tactics for automating your favorite project.
- Hoogle for Lean
- The Lean API provides functions/tactics for traversing the environment (
environment.fold), type inference (tactic.infer_type), unification (tactic.unify), etc.
- The Lean API provides functions/tactics for traversing the environment (
- Documentation generator. The tactic
tactic.doc_stringretrieves the doc string for a given declaration. - Goal visualizer. VS Code can render complex graphics and elaborated formatting, it is built on top of Chromium.
The Lean goal pretty printer can be customized, we just need to define our instance for
has_to_format tactic_state. - Type based auto completion. The idea is to filter the list of candidates using the expected type.
- Formatting tool. Build a tool to automatically format Lean code using a consistent rule set. Consider similar tools.
- Debugger interface based on the VM monitoring API. Consider using the VS Code generic debug UI.
Thank you
- Website: http://leanprover.github.io/
- Source code: https://github.com/leanprover/lean
- Lean discussion group: https://groups.google.com/forum/#!forum/lean-user