The Lean Theorem Prover
and
Automation

Leonardo de Moura (Microsoft Research)

CPP, 2016/01/19
http://leanprover.github.io/

The Lean Theorem Prover Team

  • Soonho Kong (CMU),
  • Jeremy Avigad (CMU)
  • Floris van Doorn (CMU),
  • Rob Lewis (CMU),
  • Jakob von Raumer (KIT),
  • Daniel Selsam (Stanford)

Many thanks to

  • Cody Roux
  • Georges Gonthier
  • Grant Passmore
  • Nikhil Swamy
  • Assia Mahboubi
  • Bas Spitters
  • Steve Awodey
  • Ulrik Buchholtz
  • Tom Ball
  • Parikshit Khanna
  • Haitao Zhang

Introduction: Lean

  • New open source theorem prover
  • Platform for
    • Software verification & development
    • Formalized mathematics
    • Education (mathematics, logic, computer science)
    • Synthesis (proofs & programs)
  • de Bruijn's Principle: small trusted kernel
  • Expressive logic
  • Partial constructions: automation fills the "holes"

Introduction: Lean

Main Goal

Lean aims to bring two worlds together

  • An interactive theorem prover with powerful automation
  • An automated reasoning tool that
    • produces (detailed) proofs,
    • has a rich language,
    • can be used interactively, and
    • is built on a verified mathematical library

Secondary Goals

  • Robust proofs
  • Minimalist and high-performace kernel
  • Education
    • Interactive courses
    • Proving should be as easy as programming
  • Have Fun

Software verification and
Formalized Mathematics

Software verification and
Formalized Mathematics

  • Similar problems
    • Proof stability
    • Libraries are big
    • Scalability issues
    • Finding existing functions/theorems
  • Common problems in software engineering:
    • Every attempt to create a single unified language failed (ADA?)
    • We keep reimplementing the same libraries over and over again
    • Mixing libraries from different languages is usually a mess
    • Bit rotting
  • These problems also affect formalized mathematics

What is new?

  • Poweful elaboration engine that can handle
    • Higher-order unification
    • Definitional reductions
    • Coercions
    • Ad-hoc polymorphism (aka overloading)
    • Type classes
    • Tactics

"By relieving the brain of all unnecessary work, a good notation sets it free to concentrate on more advanced problems, and in effect increases the mental power of the race." – A. N. Whitehead

What is new?

  • Poweful elaboration engine that can handle
  • Small trusted kernel
    • It does not contain
      • Termination checker
      • Fixpoint operators
      • Pattern matching
      • Module management

What is new?

  • Poweful elaboration engine that can handle
  • Small trusted kernel
  • Multi-core support
    • Process theorems in parallel
    • Execute/try tactics (automation) in parallel

What is new?

  • Poweful elaboration engine that can handle
  • Small trusted kernel
  • Multi-core support
  • Fast incremental compilation

What is new?

  • Poweful elaboration engine that can handle
  • Small trusted kernel
  • Multi-core support
  • Fast incremental compilation
  • Support for mixed declarative and tactic proof style

What is new?

  • Poweful elaboration engine that can handle
  • Small trusted kernel
  • Multi-core support
  • Fast incremental compilation
  • Support for mixed declarative and tactic proof style
  • Automation

Dependent Type Theory

  • Before we started Lean, we have studied different theorem provers: ACL2, Agda, Automath, Coq, HOL (family), Isabelle, Mizar, PVS
  • Dependent type theory is really beautiful
  • Some advantages
    • Bultin computational interpretation
    • Same data-structure for representing proofs and terms
    • Reduce code duplication, example:
      • We implemented a compiler for Haskell-like recursive equations, we can use it to construct proofs by induction
    • Mathematical structures (such as Groups and Rings) are first-class citizens
  • Some references

Architecture

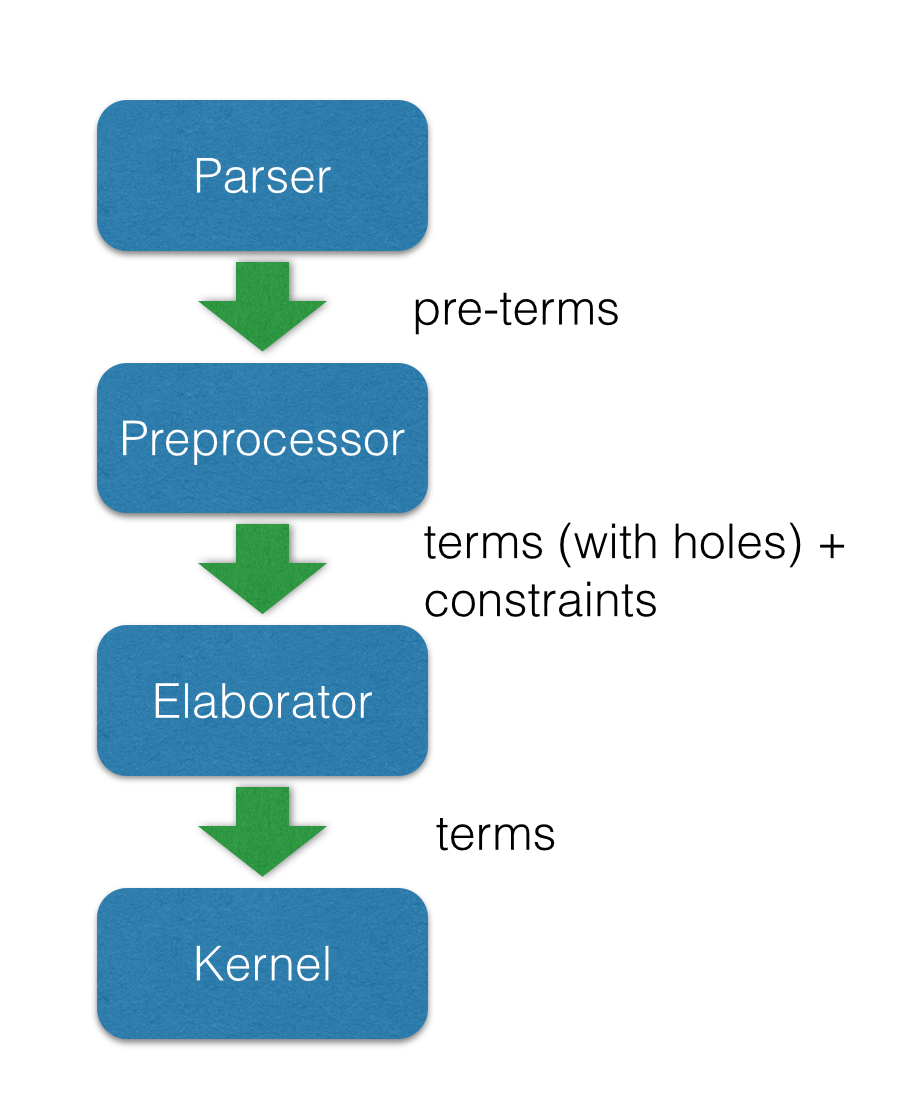
framework1.png

Architecture

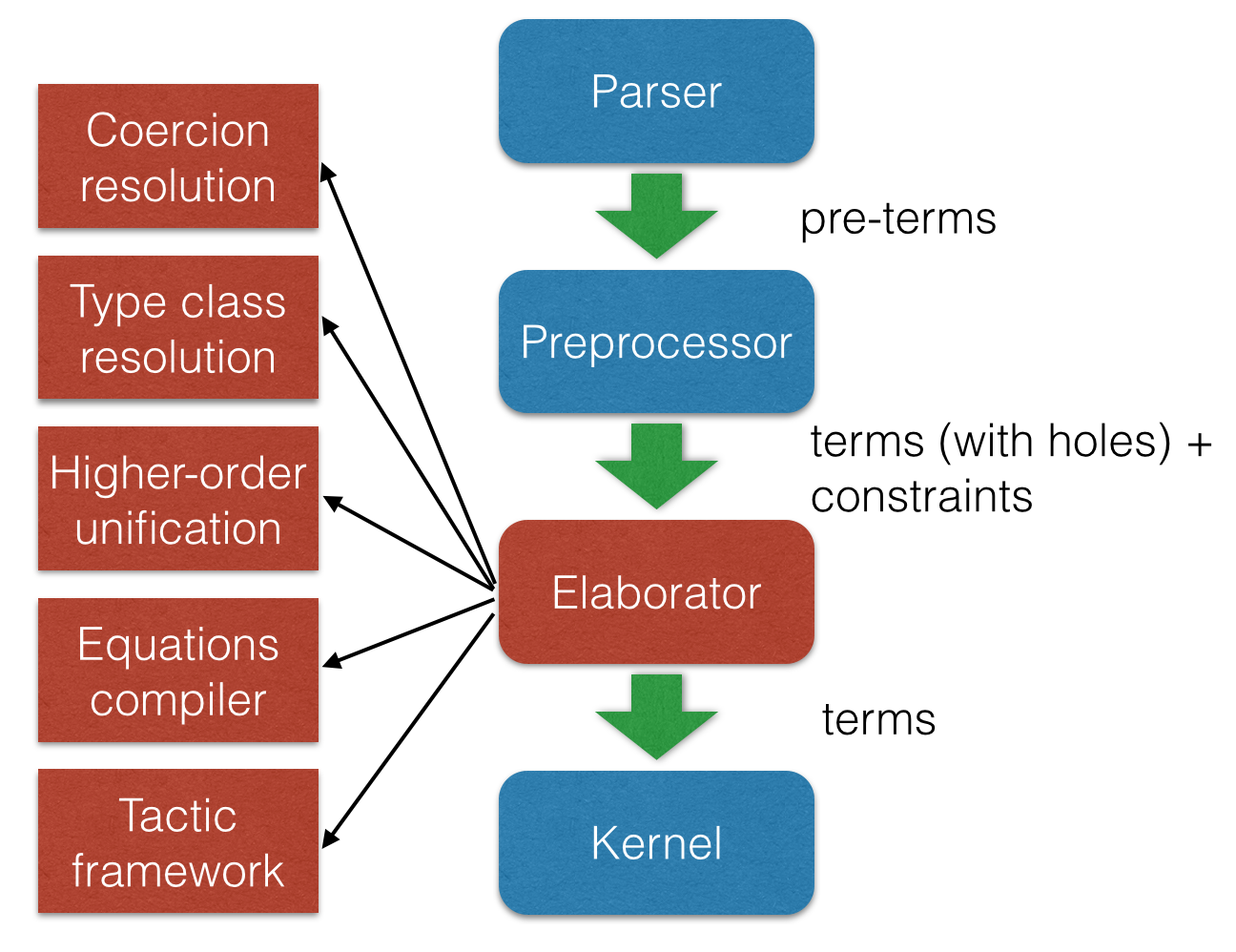
framework2.png

Kernel

  • Kernel is implemented in two layers for easy customization

  • 1st layer, dependent lambda calculus + options:

    • Proof irrelevance
    • Impredicative Prop
    Π (x : nat), x = x -- is a Proposition ∀ (x : nat), x = x -- Alternative notation
  • 2nd layer: Inductive families, Quotient types, HITs

kernel.png

Two official libraries

  • Standard
    • Proof irrelevant and impredicative Prop
    • Smooth transition to classical logic
    • Inductive Families
    • Quotient Types
  • HoTT
    • Proof relevant and no impredicative Prop
    • Univalence axiom
    • Inductive Families
    • HIT
  • Easy to implement experimental versions, Example: Steve Awodey asked for proof relevant and impredicative universe

Agnostic Mathematics

  • Support constructive and classical mathematics
  • Computation is important to mathematics
  • Core parts of the standard library are constructive
  • Separation of concerns:
    • Methods to write computer programs
    • Freedom to use a nonconstructive theories and methods to reason about them

Noncomputable Keyword

  • Our conjecture: most users don't care about constructivism, what they really care about is whether code can be generated our not for a definition.
private noncomputable definition pb {s : seq} (Hs : regular s) (Hpos : pos s) := some (abs_pos_of_nonzero Hs (sep_zero_of_pos Hs Hpos)) private noncomputable definition ps {s : seq} (Hs : regular s) (Hsep : sep s zero) := some (abs_pos_of_nonzero Hs Hsep) noncomputable definition s_inv {s : seq} (Hs : regular s) (n : ℕ+) : ℚ := if H : sep s zero then (if n < (ps Hs H) then 1 / (s ((ps Hs H) * (ps Hs H) * (ps Hs H))) else 1 / (s ((ps Hs H) * (ps Hs H) * n))) else 0

Freedom to trust

  • Option: type check imported modules.
  • Macros: semantic attachments for speeding up type checking and evaluation.
  • Macros can be eliminated (expanded into pure Lean code).
  • Each macro provides a function for computing the type and evaluating an instance.
  • Each macro can be assigned a trust level.
  • Many applications: interface with the GNU multiprecision arithmetic (GMP) library.

Freedom to trust

  • Relaxed mode
    • Trust the imported modules have not been tampered
    • Trust all macros
  • Paranoid mode
    • Retype check all imported modules (someone may have changed the binaries)
    • Expand all macros (the developers may have made mistakes, GMP may be buggy)
  • Stronger guarantee Retype check everything using Lean reference type checker

Exporting libraries

Recursive equations

  • Recursors are inconvenient to use.
  • Compiler from recursive equations to recursors.
  • Two compilation strategies: structural and well-founded recursion
definition fib : nat → nat | fib 0 := 1 | fib 1 := 1 | fib (a+2) := fib (a+1) + fib a example (a : nat) : fib (a+2) = fib (a+1) + fib a := rfl
  • Proofs by induction

Recursive equations

  • Dependent pattern matching
definition map {A B C : Type} (f : A → B → C) : Π {n : nat}, vector A n → vector B n → vector C n | map nil nil := nil | map (a::va) (b::vb) := f a b :: map va vb definition zip {A B : Type} : Π {n}, vector A n → vector B n → vector (A × B) n | zip nil nil := nil | zip (a::va) (b::vb) := (a, b) :: zip va vb

Human-readable proofs

import algebra.category open eq.ops category functor natural_transformation variables {ob₁ ob₂ : Type} {C : category ob₁} {D : category ob₂} {F G H : C ⇒ D} definition nt_compose (η : G ⟹ H) (θ : F ⟹ G) : F ⟹ H := natural_transformation.mk (take a, η a ∘ θ a) (take a b f, calc H f ∘ (η a ∘ θ a) = (H f ∘ η a) ∘ θ a : assoc ... = (η b ∘ G f) ∘ θ a : naturality ... = η b ∘ (G f ∘ θ a) : assoc ... = η b ∘ (θ b ∘ F f) : naturality ... = (η b ∘ θ b) ∘ F f : assoc

Tactics

  • Automation such as rewrite engined, simplifiers and decision procedures are integrated into the system as tactics.
  • A placeholder/hole can be viewed as a goal
  • A proof state is a sequence of goals, substitution (already solved holes), and postponed constraints.
  • A tactic is a function from proof state to a lazy stream of proof states (very similar to Isabelle).
  • Tacticals are tactic combinadors: andthen, orelse, par, …

Structures

  • Special kind of inductive datatype (only one constructor)
  • Projections are generated automatically
  • "Inheritance"
  • Extensively used to formalize the algebraic hierarchy
  • We can view them as parametric modules
structure has_mul [class] (A : Type) := (mul : A → A → A) structure semigroup [class] (A : Type) extends has_mul A := (mul_assoc : ∀a b c, mul (mul a b) c = mul a (mul b c)) ... structure group [class] (A : Type) extends monoid A, has_inv A := (mul_left_inv : ∀a, mul (inv a) a = one)

Structures

structure ring [class] (A : Type) extends add_comm_group A, monoid A, distrib A variable {A : Type} theorem ring.mul_zero [s : ring A] (a : A) : a * 0 = 0 := have H : a * 0 + 0 = a * 0 + a * 0, from calc a * 0 + 0 = a * 0 : by simp ... = a * (0 + 0) : by simp ... = a * 0 + a * 0 : by simp show a * 0 = 0, by simp

Structures (additional instances)

structure ring [class] (A : Type) extends add_comm_group A, monoid A, distrib A variable {A : Type} theorem ring.mul_zero [s : ring A] (a : A) : a * 0 = 0 := ... theorem ring.zero_mul [s : ring A] (a : A) : 0 * a = 0 := ... definition ring.to_semiring [instance] [s : ring A] : semiring A := ⦃ semiring, s, mul_zero := ring.mul_zero, zero_mul := ring.zero_mul ⦄

Structures (concrete instances)

protected definition int.linear_ordered_comm_ring [instance] : algebra.linear_ordered_comm_ring int := ⦃algebra.linear_ordered_comm_ring, int.integral_domain, le := int.le, le_refl := int.le.refl, le_trans := int.le.trans, le_antisymm := int.le.antisymm, lt := int.lt, le_of_lt := int.le_of_lt, lt_irrefl := int.lt.irrefl, ... le_iff_lt_or_eq := int.le_iff_lt_or_eq, le_total := int.le.total, zero_ne_one := int.zero_ne_one, zero_lt_one := int.zero_lt_one, add_lt_add_left := int.add_lt_add_left⦄
  • Is int a add_group? Yes
int.linear_ordered_comm_ring : algebra.linear_ordered_comm_ring int linear_ordered_comm_ring int → comm_ring int comm_ring int → ring int ring int → add_comm_group int add_comm_group int → add_group int

Sylow theorem

variables {A : Type} [group A] [fintype A] [decidable_eq A] include ambA deceqA finA theorem cauchy_theorem : ∀ p, prime p → p ∣ card(A) → ∃ g : A, order(g) = p theorem first_sylow_theorem : ∀ p, prime p → ∀ n, p^n ∣ card(A) → ∃ (H : finset A) (sg : is_finsubg H), card(H) = p^n

Automation in Lean

  • Joint work with Daniel Selsam (Stanford)
  • Work in Progress
  • Collection of proof procedures
    • Congruence closure
    • E-matching
    • Arithmetic
    • Ordered rewriting
    • Completion and superposition calculus
  • SMT/ATP procedures for dependent type theory.
  • Indexing

Automation (main challenges)

  • Many different settings
    • Constructive vs Classical
    • Semi-constructive axioms: propext, quotients/funext
    • Proof relevant vs proof irrelevant
    • Impredicative Prop
  • Dependent types
  • Type classes
theorem mul.assoc [semigroup A] (a b c : A) : a * b * c = a * (b * c)

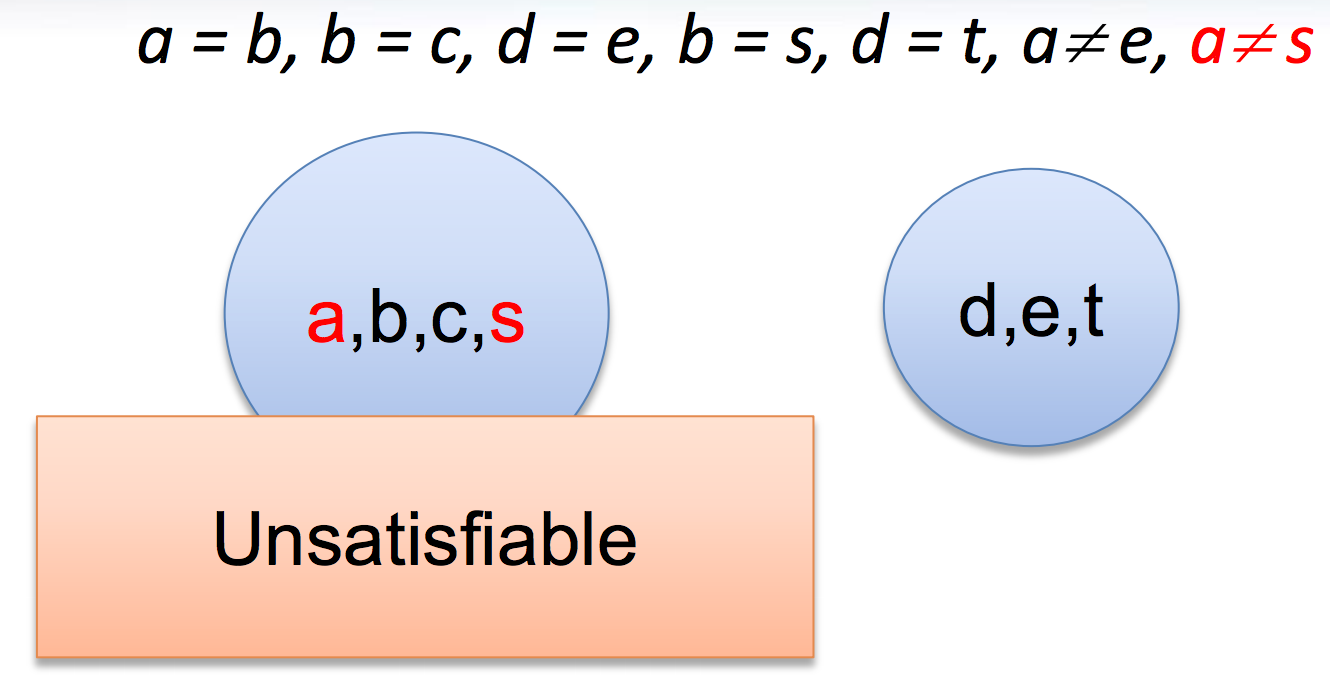
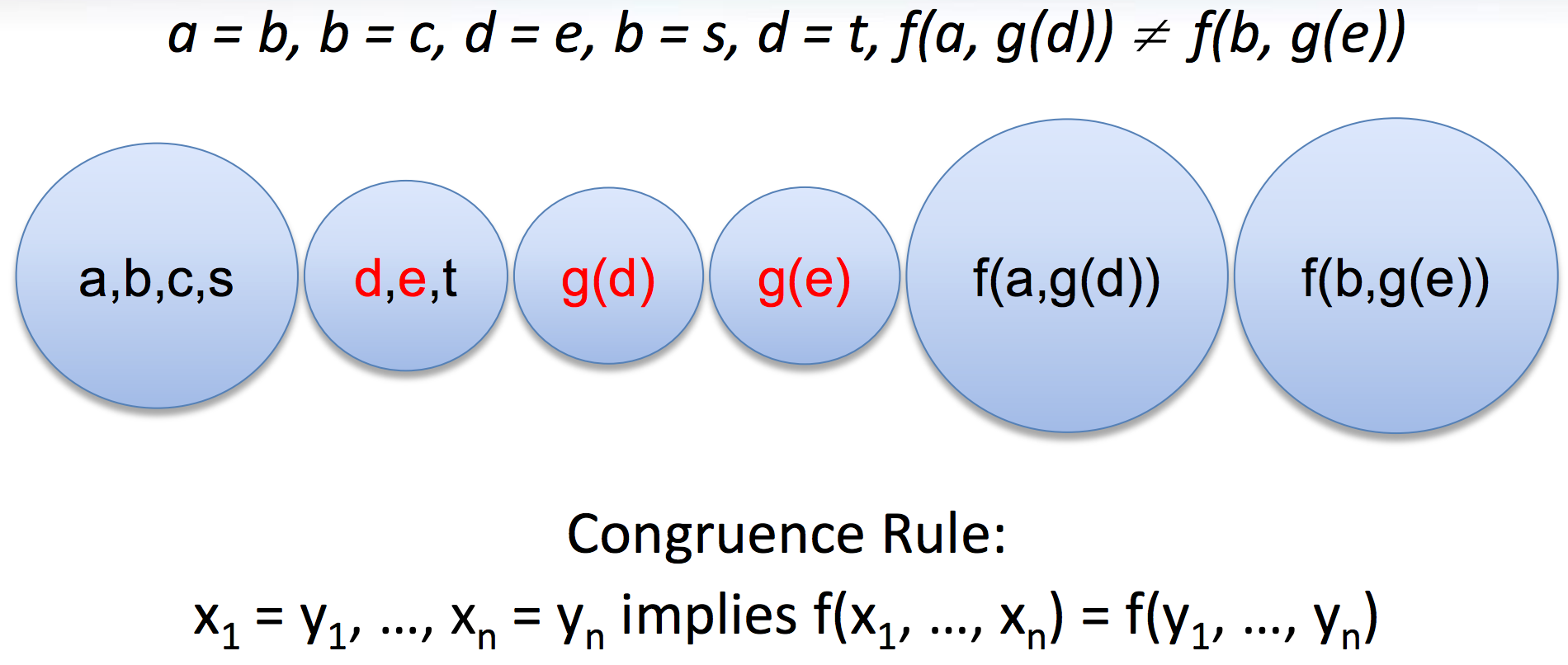
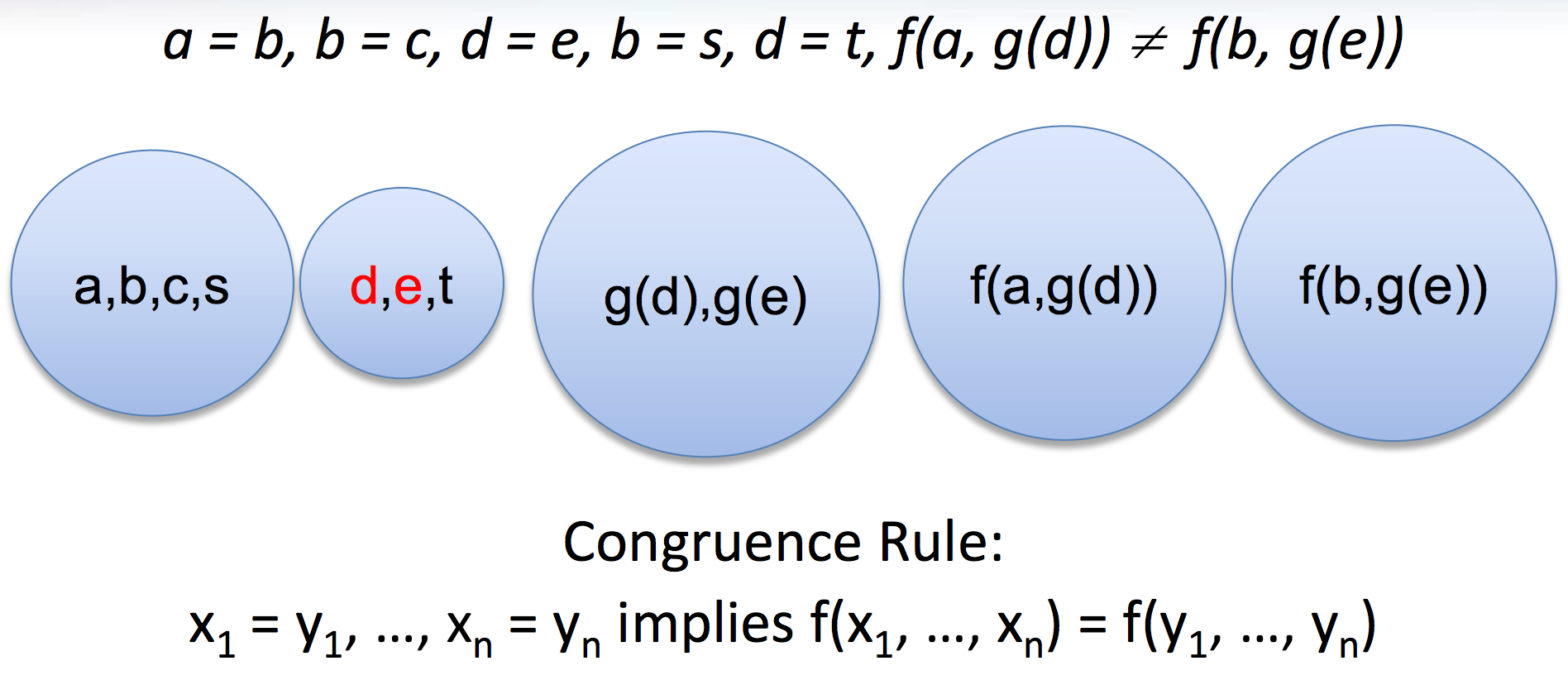
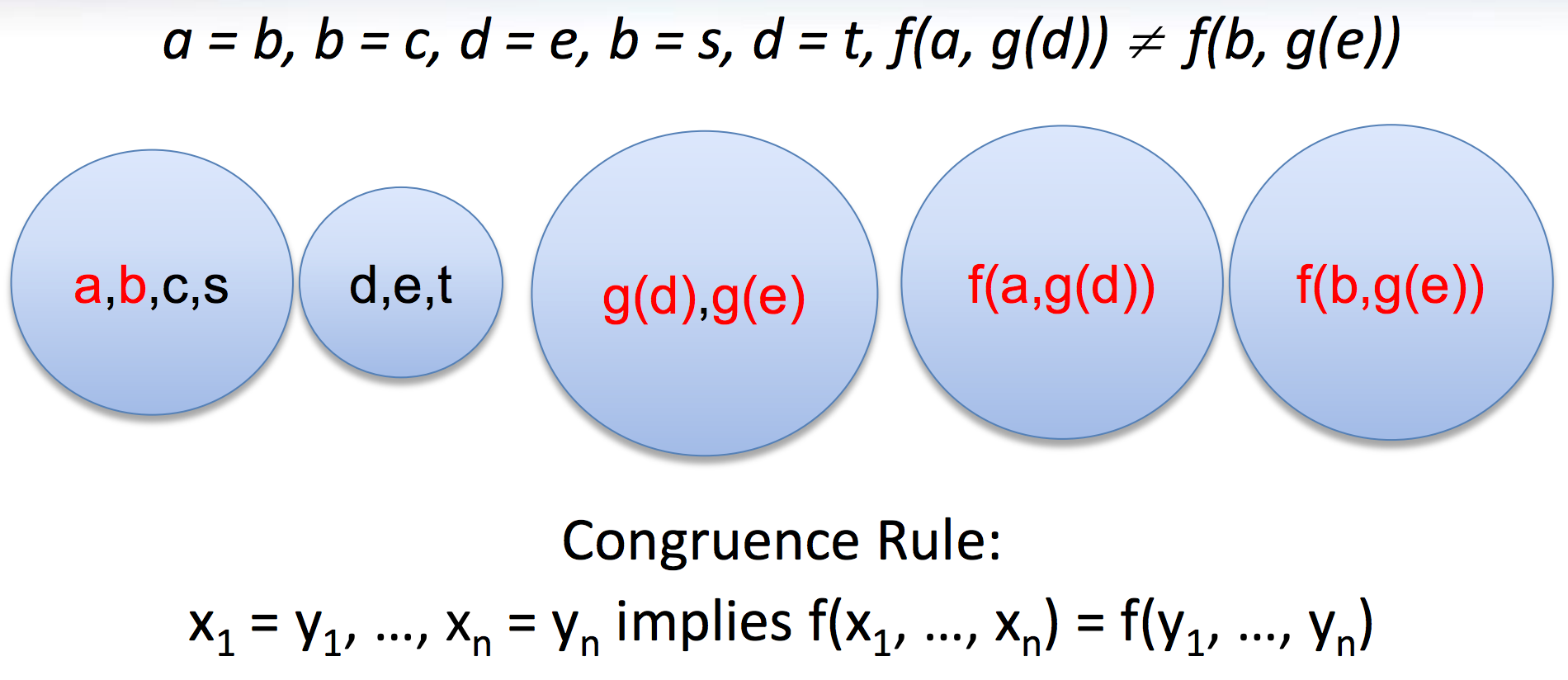
Congruence closure

  • It is in the kernel of most SMT solvers (e.g., CVC4, MathSAT, Yices, Z3)
  • Efficient procedure for equality

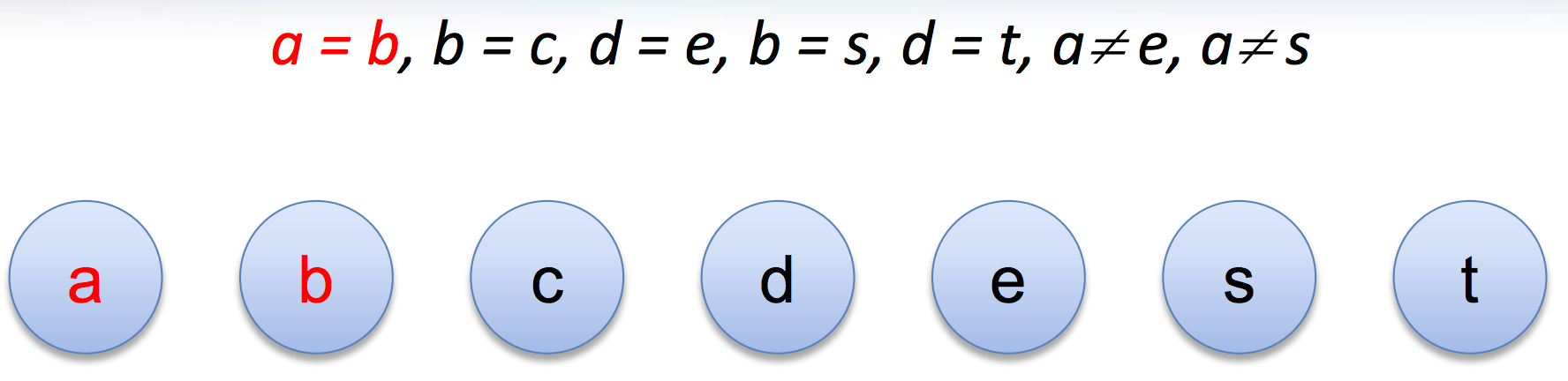
cc1.png

Congruence closure

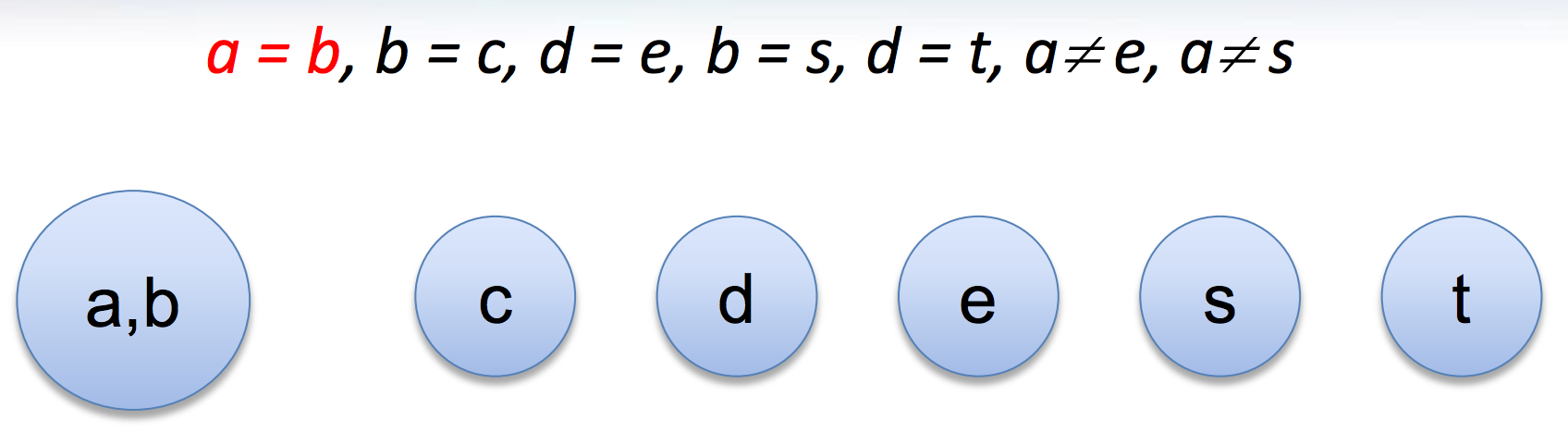
cc2.png

Congruence closure

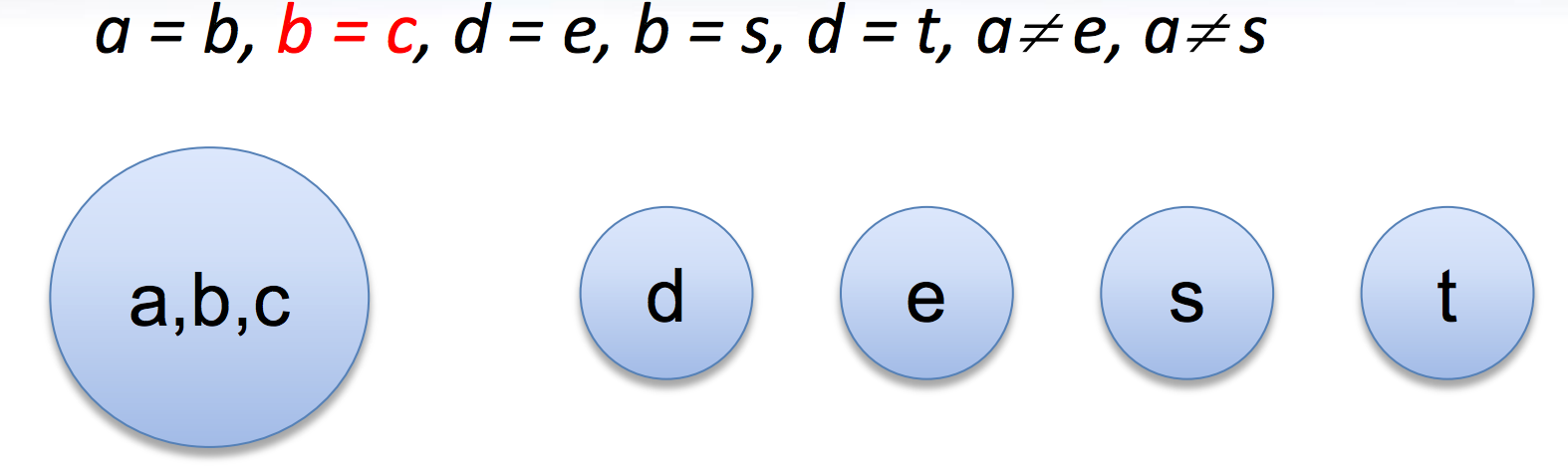
cc3.png

Congruence closure

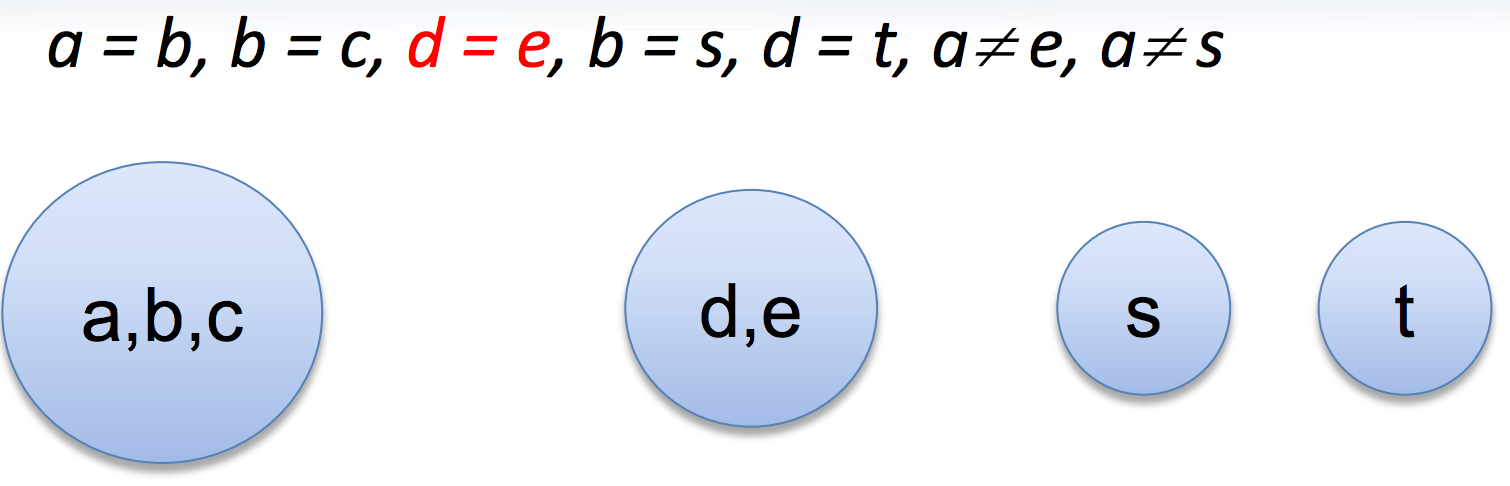
cc4.png

Congruence closure

cc5.png

Congruence closure

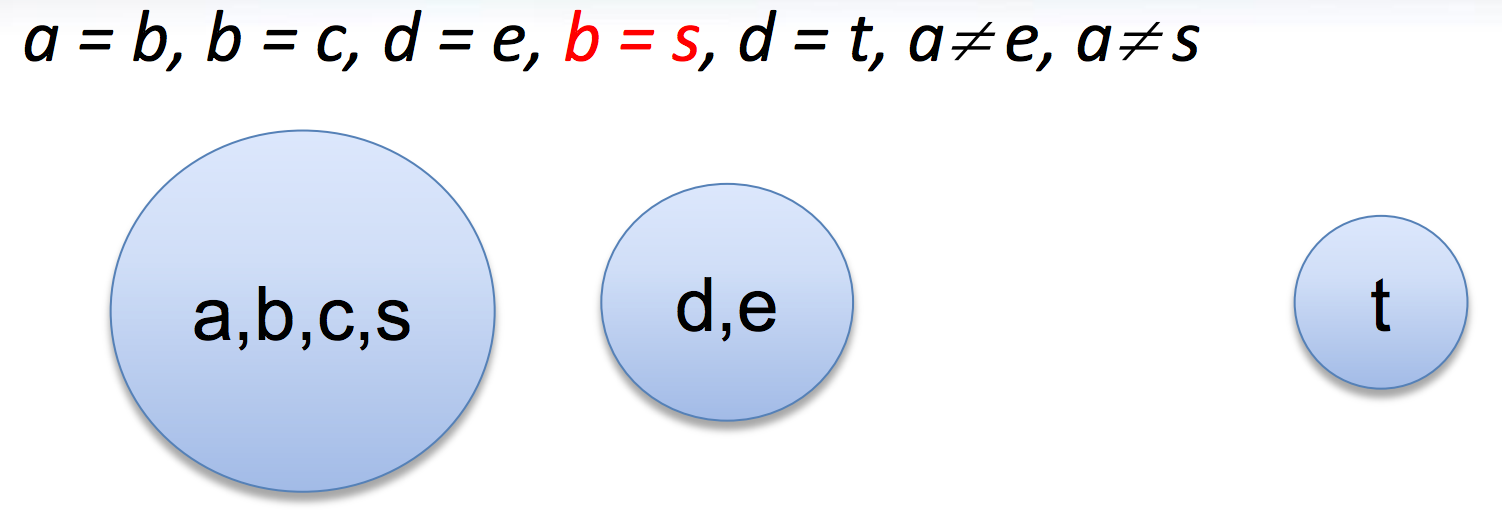
cc6.png

Congruence closure

cc7.png

Congruence closure

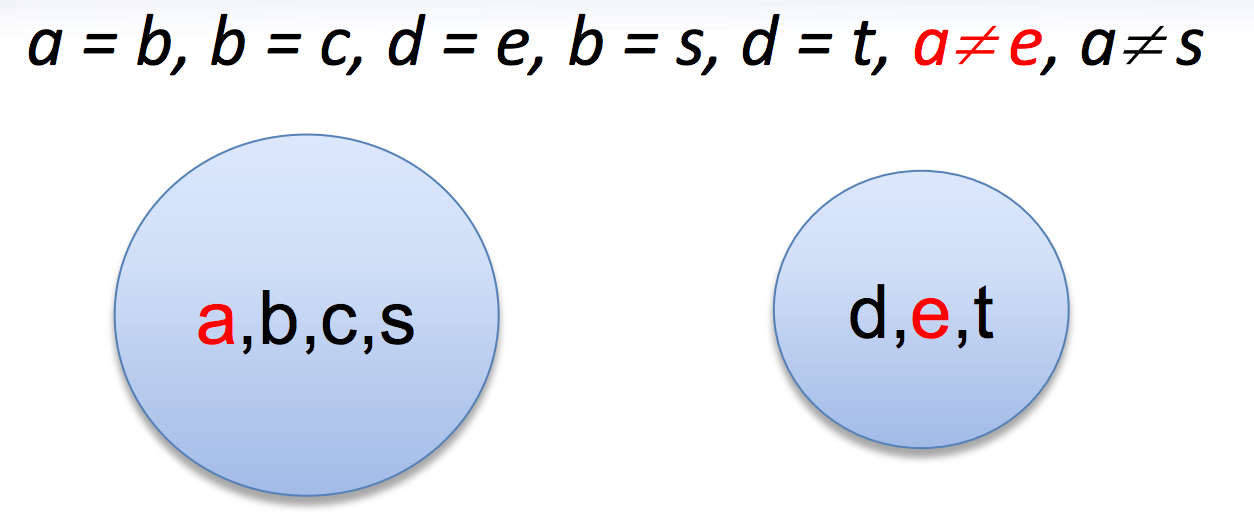
cc8.png

Congruence closure

cc9.png

Congruence closure

cc10.png

Congruence closure

cc11.png

Congruence closure

cc12.png

Congruence closure

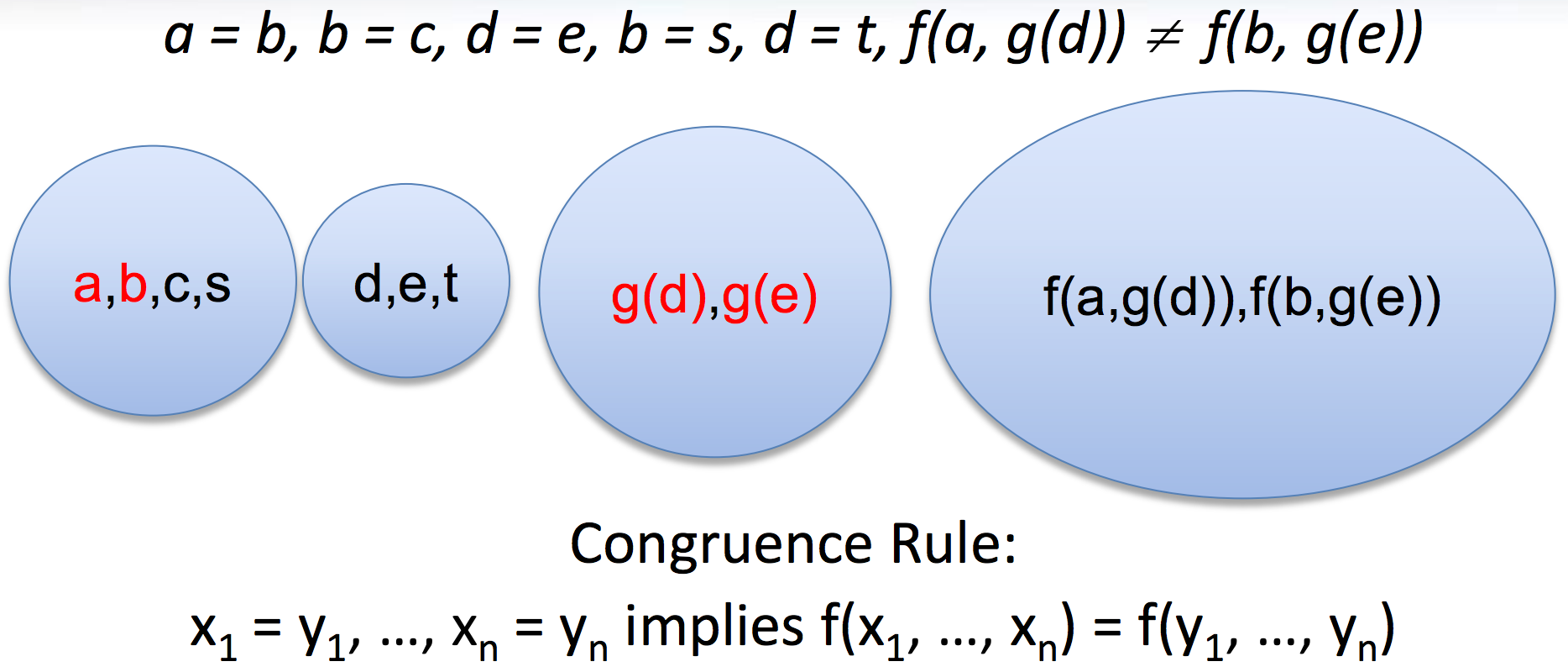
cc13.png

Congruence closure + Heuristic instantiation

  • Heuristic instantiation: adds instances of lemmas to local context.
  • Simple and effective (used by many SMT solvers).
  • "Context as a black board".
  • Indexing.
  • Avoids many technical issues.

Congruence closure and dependent functions

  • Equality type
variables A : Type variables a b : A a = b -- is notation for eq A a b
  • Congruence closure is easy for non-dependent functions.
lemma congr {A B : Type} {f g : A → B} {a b : A} : f = g → a = b → f a = g b
  • Dependent functions
variables (A : Type) (B : A → Type) (f : Π a : A, B a) variables (a b : A) -- The following equality is not type correct check f a = f b check f a : B a check f b : B b

Casts

  • Cast operation
variables (e : a = b) (t : B a) check e ▸ t -- e ▸ t : B b
lemma dcongr {A : Type} {B : A → Type} {f g : Π a : A, B a} {a b : A} (e₁ : f = g) (e₂ : a = b) : e₂ ▸ (f a) = g b

Heterogeneous equality

variables A B : Type variables a : A variables b : B a == b -- is notation for heq A a B b
lemma dcongr {A : Type} {B : A → Type} {f g : Π a : A, B a} {a b : A} (e₁ : f = g) (e₂ : a = b) : f a == g b
  • Heterogeneous to Homogeneous
variables A : Type variables a b : A a == b → a = b -- We need UIP, K-axiom or proof irrelevance

Congruence for heterogeneous equality

  • Next problem: following lemma is not provable without assuming another axiom.
lemma hcongr {A A' : Type} {B : A → Type} {B' : A' → Type} {f : Π a : A, B a} {g : Π a : A', B' a} {a : A} {b : A'} : f == g → a == b → f a == g b

Congruence for heterogeneous equality

  • BUT, the following family of lemmas is
lemma hcongr_n {A₁ : Type} {A₂ : A₁ → Type} ... (f g: Π a_1 ... a_n, B a_1 ... a_n) : f = g → a_1 == b_1 → ... → a_n == b_n → f a_1 ... a_n == f b_1 ... b_n

Example

  • Induction + Congruence closure + Heuristic instantiation is already quite useful.
inductive vector (A : Type) : nat → Type := | nil {} : vector A zero | cons : Π {n}, A → vector A n → vector A (succ n) definition append : Π {n m : nat}, vector A n → vector A m → vector A (n + m) | 0 m [] w := w | (succ n) m (a::v) w := a :: (append v w) notation ⟨ a ⟩ := cast (by blast) a definition reverse : Π {n : nat}, vector A n → vector A n | 0 [] := [] | (succ n) (x :: xs) := ⟨ reverse xs ++ [x] ⟩ theorem reverse_reverse : ∀ {n : nat} (v : vector A n), reverse (reverse v) = v := by blast theorem reverse_append : ∀ {n m : nat} (v : vector A n) (w : vector A m), reverse (append v w) == append (reverse w) (reverse v) := by blast

Congruence closure and proof relevance

  • In HoTT mode (proof relevant), the previous solution doesn't work.
  • No general solution so far.
  • The basic idea is the same: generate custom congruence lemmas.
  • We can handle many special cases.
  • Examples:
    • Indices are h-Sets (nat is a hSet).
    • Parameters that are mere propositions (h-Props) can be ignored.

Future work

  • More automation
  • Efficient evaluator
  • Code generator
  • Better libraries (ongoing work)

Thank you