The Lean Theorem Prover

Leonardo de Moura (Microsoft Research),
Soonho Kong (CMU), Jeremy Avigad (CMU),
Floris van Doorn (CMU), Jakob von Raumer (KIT),
Rob Lewis (CMU), Haitao Zhang,
Daniel Selsam (Stanford)

CADE Tutorial, 2015/08/03
http://leanprover.github.io

Many thanks to

  • Cody Roux
  • Georges Gonthier
  • Grant Passmore
  • Nikhil Swamy
  • Assia Mahboubi
  • Bas Spitters
  • Steve Awodey
  • Ulrik Buchholtz
  • Tom Ball
  • Parikshit Khanna

Introduction: Lean

  • New open source theorem prover
  • Platform for
    • Software verification & development
    • Formalized mathematics
    • Education (mathematics, logic, computer science)
    • Synthesis (proofs & programs)
  • de Bruijn's Principle: small trusted kernel
  • Expressive logic
  • Partial constructions: automation fills the "holes"

Introduction: Lean

Main Goal

Lean aims to bring two worlds together

  • An interactive theorem prover with powerful automation
  • An automated reasoning tool that
    • produces (detailed) proofs,
    • has a rich language,
    • can be used interactively, and
    • is built on a verified mathematical library

Secondary Goals

  • Minimalist and high-performace kernel
  • Experiment with different flavors of type theory
    • Proof irrelevant vs Proof relevant
    • Impredicative vs Predicative
    • Higher Inductive Types
    • Quotient Types
    • Observational Type Theory
  • Education
    • Interactive courses
    • Proving should be as easy as programming
  • Have Fun

Software verification and
Formalized Mathematics

Software verification and
Formalized Mathematics

  • Similar problems
    • Proof stability
    • Scalability issues
    • Libraries are big
    • Finding existing functions/theorems

What is new?

  • Poweful elaboration engine that can handle
    • Higher-order unification
    • Definitional reductions
    • Coercions
    • Ad-hoc polymorphism (aka overloading)
    • Type classes
    • Tactics

"By relieving the brain of all unnecessary work, a good notation sets it free to concentrate on more advanced problems, and in effect increases the mental power of the race." – A. N. Whitehead

What is new?

  • Poweful elaboration engine that can handle
  • Small trusted kernel
    • It does not contain
      • Termination checker
      • Fixpoint operators
      • Pattern matching
      • Module management

What is new?

  • Poweful elaboration engine that can handle
  • Small trusted kernel
  • Multi-core support
    • Process theorems in parallel
    • Execute/try tactics (automation) in parallel

What is new?

  • Poweful elaboration engine that can handle
  • Small trusted kernel
  • Multi-core support
  • Fast incremental compilation

What is new?

  • Poweful elaboration engine that can handle
  • Small trusted kernel
  • Multi-core support
  • Fast incremental compilation
  • Support for mixed declarative and tactic proof style

Dependent Type Theory

  • Before we started Lean, we have studied different theorem provers: ACL2, Agda, Automath, Coq, HOL (family), Isabelle, Mizar, PVS
  • Dependent type theory is really beautiful
  • Some advantages
    • Bultin computational interpretation
    • Same data-structure for representing proofs and terms
    • Reduce code duplication, example:
      • We implemented a compiler for Haskell-like recursive equations, we can use it to construct proofs by induction
    • Mathematical structures (such as Groups and Rings) are first-class citizens
  • Some references

Dependent Type Theory

  • Constants
bool, nat, list, tree
  • Function applications
(fact n), (vector nat 10), (x + y)
  • Lambda abstractions
λ x : nat, x + 1 λ (n : nat) (v : vector nat n), cons 0 v
  • Function spaces
nat → nat Π (n : nat), vector nat n → vector nat (n+1)

Dependent Type Theory

  • What is the type of nat?
nat : Type
  • What is the type of Type?
Type : Type

Is Lean inconsistent? NO

  • Lean has a noncumulative universe hierarchy
Type.{0} : Type.{1} : Type.{2} : Type.{3} : ...
  • Supports universe polymorphism
λ (A : Type.{u}) (a : A), a
  • In ordinary situations you can ignore the universe parameters and simply write Type, leaving the "universe management" to Lean
  • examples/ex1.lean

Propositions as types

  • Propositions are types
∃ x : nat, x > 2
  • The inhabitants/elements of a proposition P are the proofs of P
  • Prop is the type of all propositions

Architecture

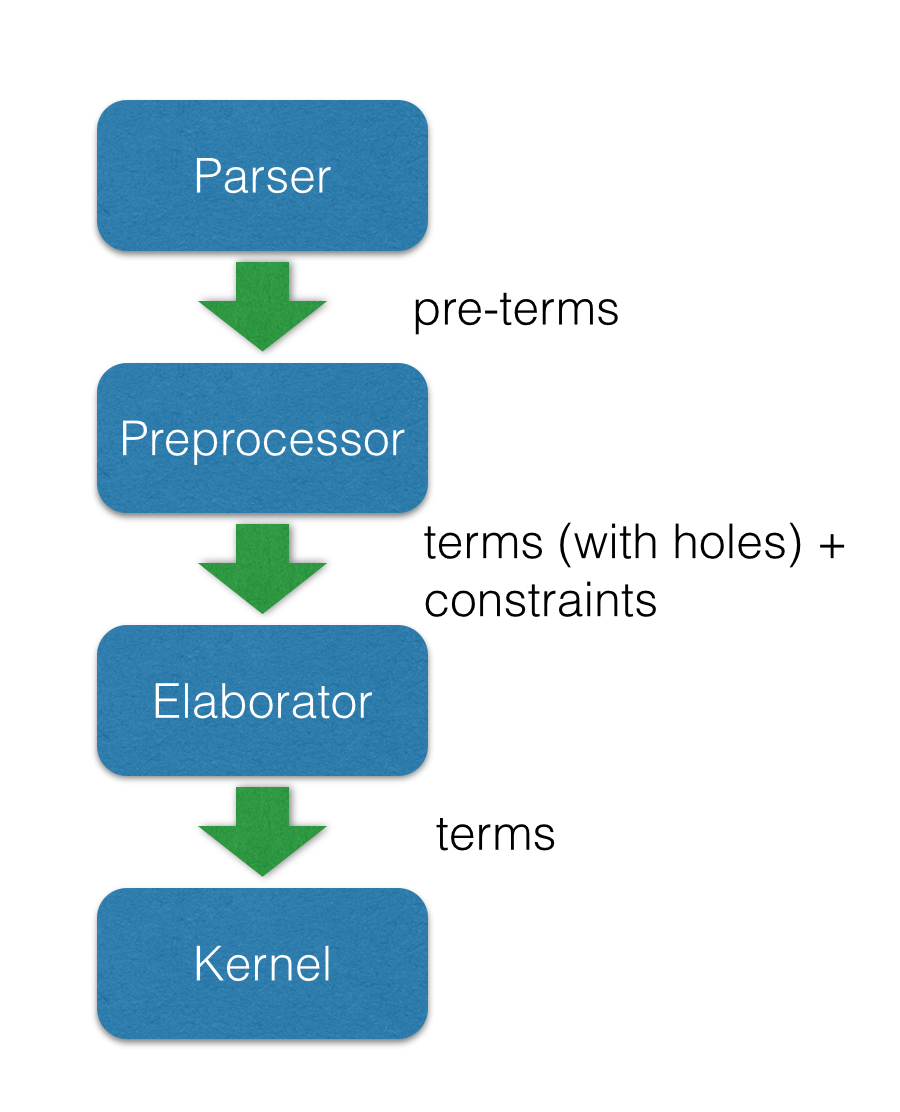
framework1.png

Architecture

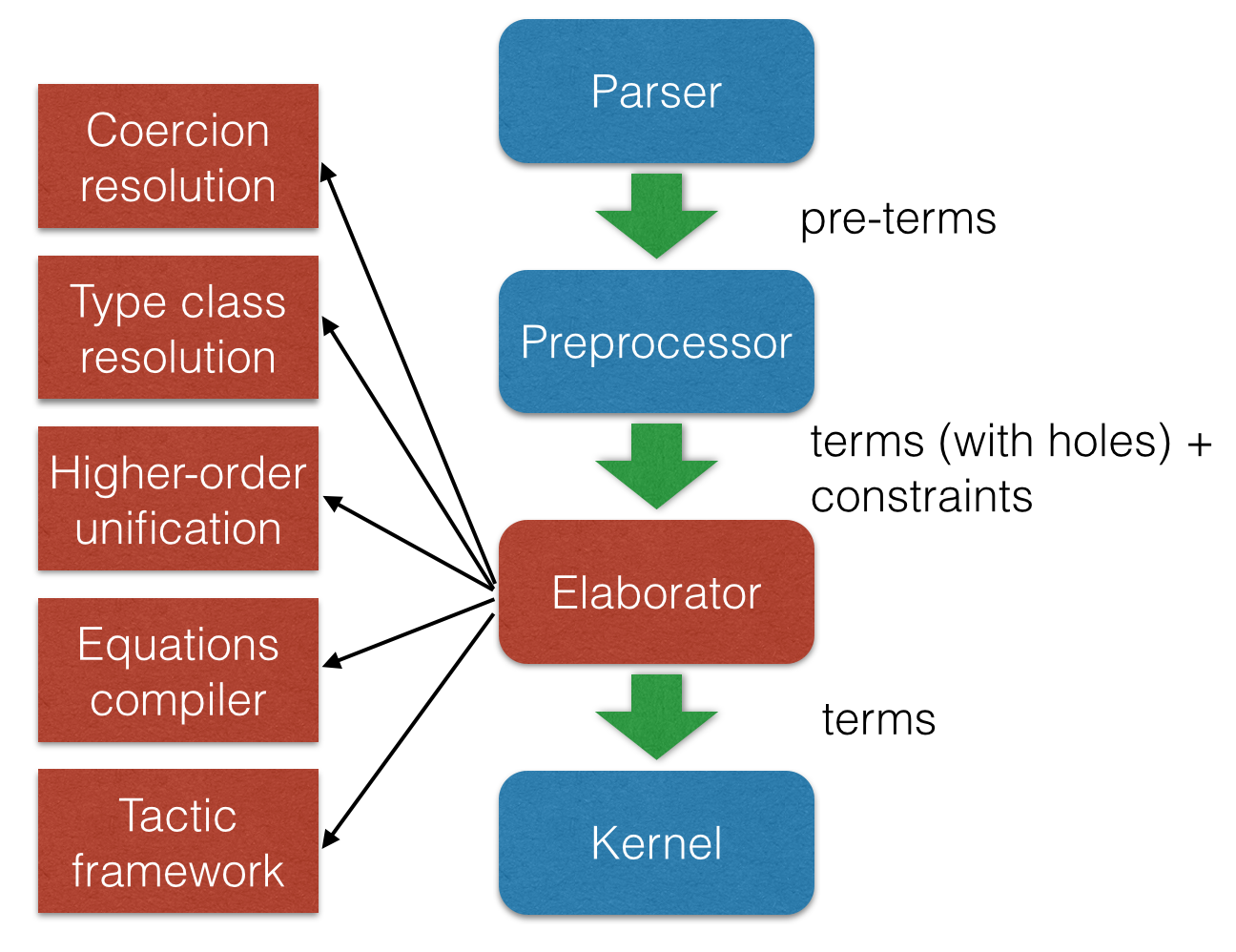
framework2.png

Architecture

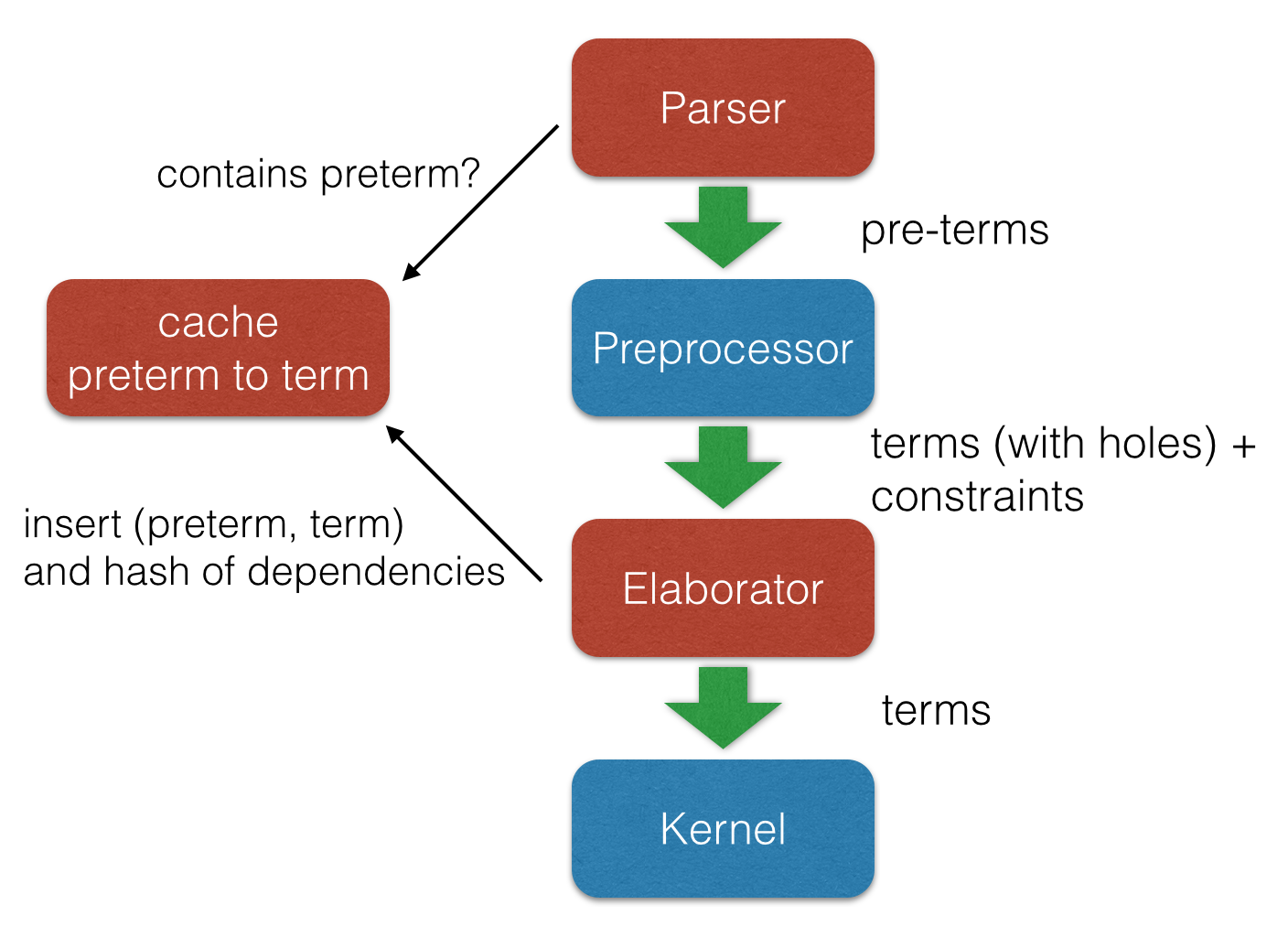
framework3.png

Kernel

  • Kernel is implemented in two layers for easy customization
  • 1st layer, dependent lambda calculus + options:
    • Proof irrelevance
    • Impredicative Prop
    Π (x : nat), x = x -- is a Proposition ∀ (x : nat), x = x -- Alternative notation
  • 2nd layer: Inductive families, Quotient types, HITs
kernel.png

Two official libraries

  • Standard
    • Proof irrelevant and impredicative Prop
    • Smooth transition to classical logic
    • Inductive Families
    • Quotient Types
  • HoTT
    • Proof relevant and no impredicative Prop
    • Univalence axiom
    • Inductive Families
    • HIT
  • Easy to implement experimental versions, Example: Steve Awodey asked for proof relevant and impredicative universe

Implicit arguments

  • Curly braces indicate that argument should be inferred rather than entered explicitly.
definition id {A : Type} (a : A) : A := a check id 10 -- @id num 10 check @id num 10

Implicit arguments

  • Elaborator uses higher-order unification.
check @eq.subst -- eq.subst : ∀ {A : Type} {a b : A} {P : A → Prop}, -- a = b → P a → P b variables (A : Type) (R : A → A → Prop) variables (a b c : A) (f : A → A → A) example (H₁ : R (f a a) (f a a)) (H₂ : a = b) : R (f a b) (f b a) := eq.subst H₂ H₁ example (H₁ : R (f a a) (f a a)) (H₂ : a = b) : R (f a b) (f b a) := @eq.subst A a b (λ x : A, R (f a x) (f x a)) H₂ H₁

Example 2

Agnostic Mathematics

  • Support constructive and classical mathematics
  • Constructive results are more informative
  • Computation is important to mathematics
  • Core parts of the standard library are constructive
  • Separation of concerns:
    • Methods to write computer programs
    • Freedom to use a nonconstructive theories and methods to reason about them

Agnostic Mathematics

  • Semi constructive axioms:
    • Function extensionality
    • Proposition extensionality
    • Quotient types (implies function extensionality)
funext: (∀ x, f x = g x) → f = g propext: (p ↔ q) → p = q
  • Computationally compatible axioms: proof irrelevant excluded middle, axiom of choice
  • Anti constructive: Hilbert's choice (aka magic)
    • consequence: all propositions are decidable

Tracking anti constructive axioms

  • We cannot generate code for anti constructive axioms such as Hilbert's choice
  • Lean provides a mechanism for checking whether a definition depends on anti constructive axioms or not.
variables {A B : Type} [h : nonempty A] noncomputable definition mk_left_inv (f : A → B) : B → A := λ b : B, if ex : (∃ a : A, f a = b) then some ex else inhabited.value (inhabited_of_nonempty h)
  • It prevents anti constructive axioms from accidentally leaking inside definitions we want to compute with (generate code for).

Axioms in the standard library

  • The standard library contains 3 axioms
propext : ∀ {a b : Prop}, (a ↔ b) → a = b quot.sound : ∀ {A : Type} [s : setoid A] {a b : A}, a ~ b → ⟦a⟧ = ⟦b⟧ strong_indefinite_description : Π {A : Type} (P : A → Prop), nonempty A → {x : A | Exists P → P x}
  • The first two axioms are semi-constructive.
  • Most of the standard library does not use these axioms.

We use propext and quot.sound for defining sets, finite sets and bags.

  • The choice axiom is used to define real division and to prove that the reals are Cauchy complete.
  • The analysis library will also be classic.

Axioms in the standard library

prop_complete : ∀ (a : Prop), a = true ∨ a = false
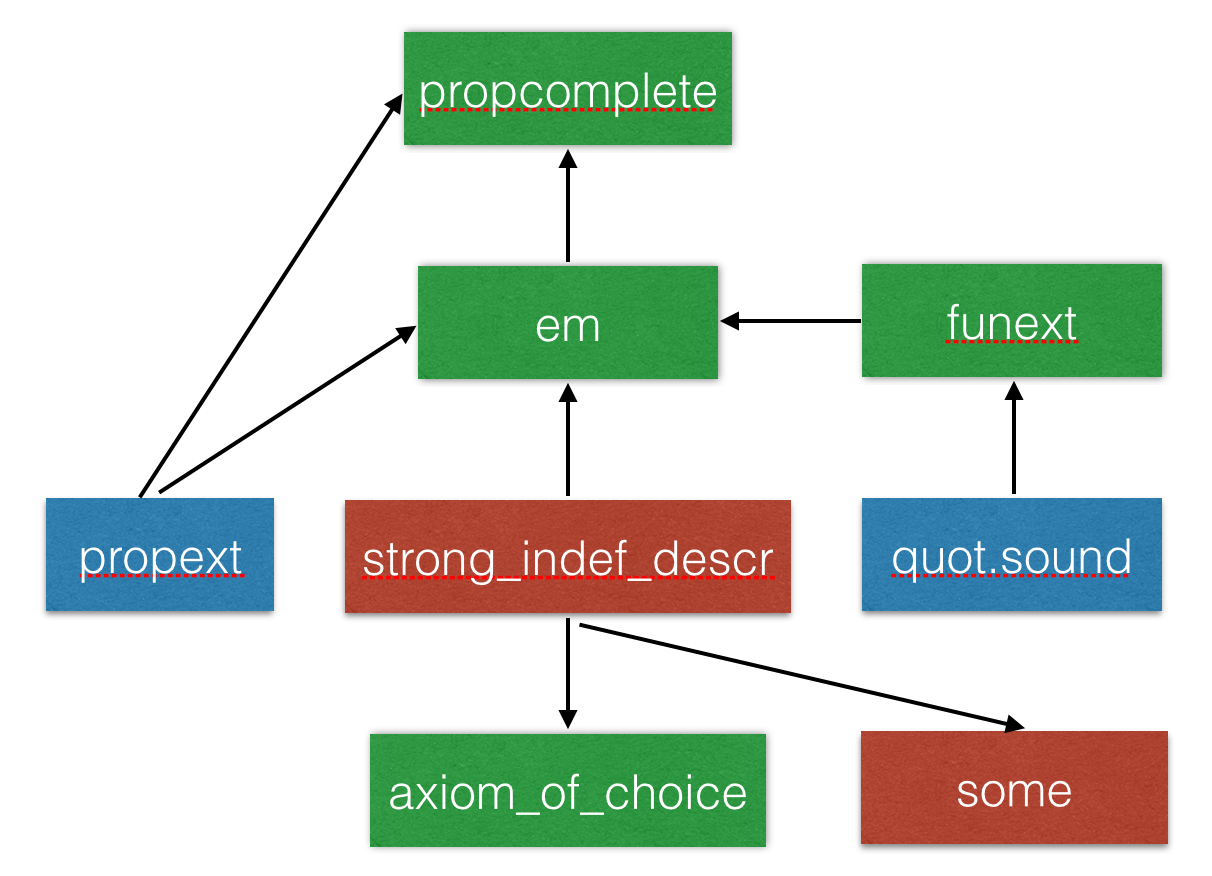
axioms.png

Freedom to trust

  • Option: type check imported modules.
  • Macros: semantic attachments for speeding up type checking and evaluation.
  • Macros can be eliminated (expanded into pure Lean code).
  • Each macro provides a function for computing the type and evaluating an instance.
  • Each macro can be assigned a trust level.
  • Many applications: interface with the GNU multiprecision arithmetic (GMP) library.

Freedom to trust

  • Relaxed mode
    • Trust the imported modules have not been tampered
    • Trust all macros
  • Paranoid mode
    • Retype check all imported modules (someone may have changed the binaries)
    • Expand all macros (the developers may have made mistakes, GMP may be buggy)
  • Stronger guarantee Retype check everything using Lean reference type checker

Reference type checker

  • Implemented by Daniel Selsam
  • < 2000 lines of Haskell code
  • Available at github
  • Code is easy to read and understand
  • It can type check the whole standard library (35K lines of Lean code) under 2 mins

Exporting libraries

Inductive families

inductive nat : Type := | zero : nat | succ : nat → nat
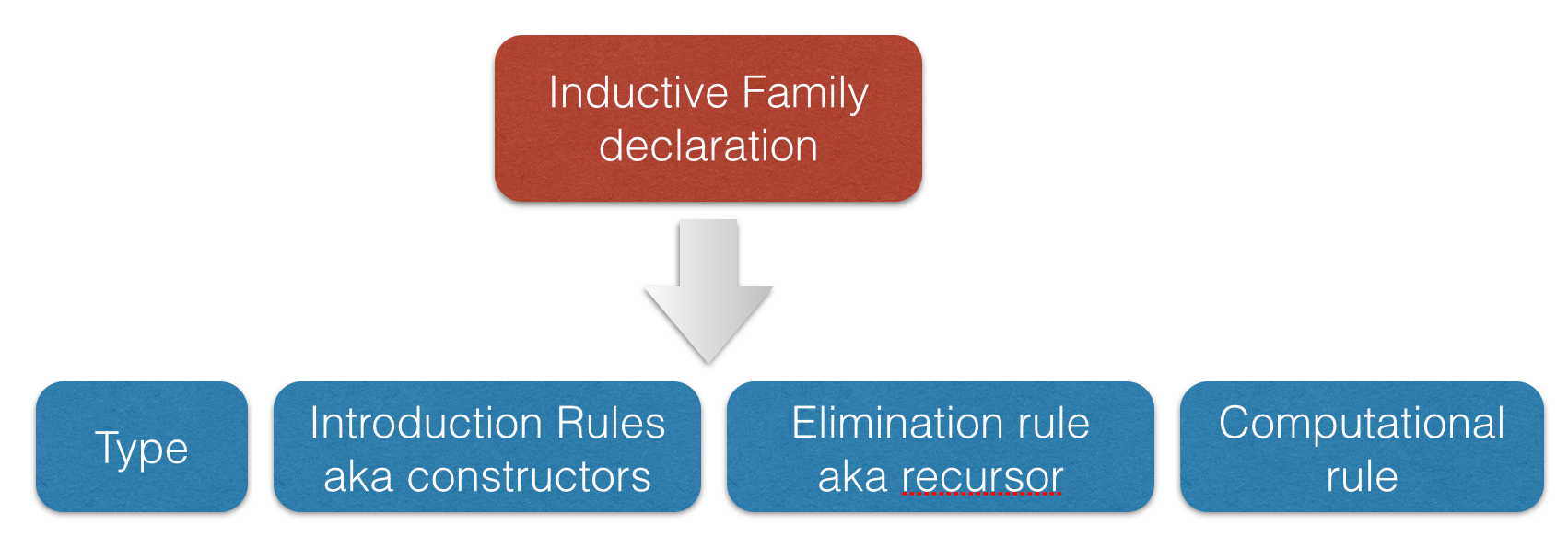
inductive.png
nat : Type nat.zero : nat -- constructor nat.succ : nat → nat -- constructor nat.rec : Π (C : nat → Type), -- recursor C nat.zero → (Π (a : nat), C a → C (nat.succ a)) → n → C n -- Computational rules nat.rec C v f nat.zero ==> v nat.rec C v f (nat.succ n) ==> f n (nat.rec C v f n)

Inductive families

definition add (x y : nat) : nat := nat.rec (λ n, nat) x (λ n r, succ r) y abbreviation C := λ n, nat abbreviation s := succ abbreviation z := zero abbreviation f := λ n r : nat, succ r add (s z) (s (s z)) = nat.rec C (s z) f (s (s z)) ... = s (nat.rec C (s z) f (s z)) ... = s (s (nat.rec C (s z) f z)) ... = s (s (s z))

Inductive families

inductive vector (A : Type) : nat → Type := | nil : vector A zero | cons : Π {n}, A → vector A n → vector A (succ n)

Inductive families

  • It is possible to construct a substantial edifice of mathematics based on nothing more than the type universes, function spaces, and inductive types; everything else follows from those.

Inductive families: auxiliary definitions

  • Lean automatically generates several auxiliary definitions whenever a new inductive family is declared.
  • examples/ex4.lean

Recursive equations

  • Recursors are inconvenient to use.
  • Compiler from recursive equations to recursors.
  • Two compilation strategies: structural and well-founded recursion
definition fib : nat → nat | fib 0 := 1 | fib 1 := 1 | fib (a+2) := fib (a+1) + fib a example (a : nat) : fib (a+2) = fib (a+1) + fib a := rfl

Recursive equations

  • Proofs by induction
theorem fib_pos : ∀ n, 0 < fib n | fib_pos 0 := show 0 < 1, from zero_lt_succ 0 | fib_pos 1 := show 0 < 1, from zero_lt_succ 0 | fib_pos (a+2) := calc 0 = 0 + 0 : rfl ... < fib (a+1) + 0 : lt_right (fib_pos (a+1)) 0 ... < fib (a+1) + fib a : lt_left (fib_pos a) (fib (a+1)) ... = fib (a+2) : rfl

Recursive equations

  • Dependent pattern matching
definition map {A B C : Type} (f : A → B → C) : Π {n : nat}, vector A n → vector B n → vector C n | map nil nil := nil | map (a::va) (b::vb) := f a b :: map va vb definition zip {A B : Type} : Π {n}, vector A n → vector B n → vector (A × B) n | zip nil nil := nil | zip (a::va) (b::vb) := (a, b) :: zip va vb

Definitional Reductions

  • Elaborator must respect the computational interpretation of terms
example (A : Type) (a b : A) : (a, b).1 = a := rfl example (A B : Type) (f : A → A → B) (a : A) : (λ x, f x x) a = f a a := rfl

Coercions

  • In Lean, we can associate attributes to definitions.
  • Coercion is one of the available attributes.
variable {A : Type} definition to_list [coercion] : ∀ {n : nat}, vector A n → list A | 0 nil := nil | (n+1) (a::v) := a::(to_list v) variable f : list nat → Prop variable v : vector nat 10 check f v -- f (@to_list nat 10 v)

Namespaces

  • We can group definitions, metadata (e.g., notation declarations and attributes) into namespaces.
  • We can open namespaces
namespace foo definition f (a : nat) := nat.succ a eval f nat.zero end foo eval foo.f nat.zero open foo eval f nat.zero open nat check 1 + 2 open nat (hiding add sub) open nat (renaming add → nadd) open nat (rec_on) open [notations] nat open -[classes] nat

Ad-hoc polymorphism

notation a + b := add a b notation a + b := bor a b eval 1 + 2 eval tt + ff
  • We can use namespaces to avoid unwanted ambiguity.
  • We can override overloading
check (#nat a + b)

Human-readable proofs

import algebra.category open eq.ops category functor natural_transformation variables {ob₁ ob₂ : Type} {C : category ob₁} {D : category ob₂} {F G H : C ⇒ D} definition nt_compose (η : G ⟹ H) (θ : F ⟹ G) : F ⟹ H := natural_transformation.mk (take a, η a ∘ θ a) (take a b f, calc H f ∘ (η a ∘ θ a) = (H f ∘ η a) ∘ θ a : assoc ... = (η b ∘ G f) ∘ θ a : naturality ... = η b ∘ (G f ∘ θ a) : assoc ... = η b ∘ (θ b ∘ F f) : naturality ... = (η b ∘ θ b) ∘ F f : assoc

Human-readable proofs

definition infinite_primes (n : nat) : {p | p ≥ n ∧ prime p} := let m := fact (n + 1) in have m ≥ 1, from le_of_lt_succ (succ_lt_succ (fact_pos _)), have m + 1 ≥ 2, from succ_le_succ this, obtain p `prime p` `p ∣ m + 1`, from sub_prime_and_dvd this, have p ≥ 2, from ge_two_of_prime `prime p`, have p > 0, from lt_of_succ_lt (lt_of_succ_le `p ≥ 2`), have p ≥ n, from by_contradiction (suppose ¬ p ≥ n, have p < n, from lt_of_not_ge this, have p ≤ n + 1, from le_of_lt (lt.step this), have p ∣ m, from dvd_fact `p > 0` this, have p ∣ 1, from dvd_of_dvd_add_right (!add.comm ▸ `p ∣ m + 1`) this, have p ≤ 1, from le_of_dvd zero_lt_one this, absurd (le.trans `2 ≤ p` `p ≤ 1`) dec_trivial), subtype.tag p (and.intro this `prime p`)

Human-readable proofs

  • have x : T, from P, C is notation for (λ x : T, C) P
  • have T, from P, C is notation for have this : T, from P, C
  • take x : T, C, is notation for λ x : T, C
  • assume x : T, C, is notation for λ x : T, C
  • suppose T, C, is notation for λ this : T, C
  • obtain w hw, from ex, C is notation for
    exists.rec (λ h hw, C) ex
  • obtain supports any inductive datatype with a single constructor
  • show T, from P is notation for (P : T)
  • `p` is notation for show p, by assumption

Type classes

  • Synthesis procedure
  • It can be viewed as a lambda-Prolog interpreter
  • Big picture
    • Mark some inductive families as classes
    • Mark some definitions as (generators of) instances
    • Indicate that some implicit arguments must be synthesized using type classes
  • Instances are treated as Horn clauses

Inhabited Type Class

inductive inhabited [class] (A : Type) : Type := mk : A → inhabited A definition default (A : Type) [h : inhabited A] : A := inhabited.rec (λ a, a) h definition prop_inhabited [instance] : inhabited Prop := inhabited.mk true definition nat_inhabited [instance] : inhabited nat := inhabited.mk nat.zero definition fun_inhabited [instance] (A B : Type) [h : inhabited B] : inhabited (A → B) := inhabited.mk (λ x : A, default B) definition prod_inhabited [instance] (A B : Type) [ha : inhabited A] [hb : inhabited B] : inhabited (A × B) := inhabited.mk (default A, default B) eval default (nat → nat × Prop) -- ⇒ λ (a : ℕ), (0, true)

Decidable Type Class

  • An element of Prop is said to be

decidable if we can decide whether it is true or false.

inductive decidable [class] (p : Prop) : Type := | inl : p → decidable p | inr : ¬p → decidable p
  • Having an element t : decidable p is stronger than having an element t : p ∨ ¬p
  • The expression if c then t else e contains an implicit argument [d : decidable c].
  • If Hilbert's choice is imported, then all propositions are decidable (smooth transition to classical reasoning).

Decidable Type Class

definition ball (n : nat) (P : nat → Prop) : Prop := ∀ x, x < n → P x definition dec_ball [instance] [H : decidable_pred P] : Π (n : nat), decidable (ball n P) | dec_ball 0 := inl (ball_zero P) | dec_ball (a+1) := match dec_ball a with | inl iH := match H a with | inl Pa := inl (ball_succ_of_ball iH Pa) | inr nPa := inr (not_ball_of_not nPa) end | inr niH := inr (not_ball_succ_of_not_ball niH) end definition is_constant_range (f : nat → nat) (n : nat) : bool := if ∀ i, i < n → f i = f 0 then tt else ff

Tactics

  • Automation such as rewrite engined, simplifiers and decision procedures are integrated into the system as tactics.
  • A placeholder/hole can be viewed as a goal
  • A proof state is a sequence of goals, substitution (already solved holes), and postponed constraints.
  • A tactic is a function from proof state to a lazy stream of proof states (very similar to Isabelle).
  • Tacticals are tactic combinadors: andthen, orelse, par, …

Tactics

  • We can switch to tactic mode using begin … end or by …
example (p q : Prop) (Hp : p) (Hq : q) : p ∧ q ∧ p := begin apply and.intro, exact Hp, apply and.intro, exact Hq, exact Hp end example (H₁ : a + 0 = 0) (H₂ : b + 0 = 0) : a + b + 0 = 0 := begin rewrite add_zero at *, rewrite [H₁, H₂] end

Structures

  • Special kind of inductive datatype (only one constructor)
  • Projections are generated automatically
  • "Inheritance"
  • Extensively used to formalize the algebraic hierarchy
  • We can view them as parametric modules
structure has_mul [class] (A : Type) := (mul : A → A → A) structure semigroup [class] (A : Type) extends has_mul A := (mul_assoc : ∀a b c, mul (mul a b) c = mul a (mul b c)) ... structure group [class] (A : Type) extends monoid A, has_inv A := (mul_left_inv : ∀a, mul (inv a) a = one)

Structures

structure ring [class] (A : Type) extends add_comm_group A, monoid A, distrib A variable {A : Type} theorem ring.mul_zero [s : ring A] (a : A) : a * 0 = 0 := have H : a * 0 + 0 = a * 0 + a * 0, from calc a * 0 + 0 = a * 0 : by rewrite add_zero ... = a * (0 + 0) : by rewrite add_zero ... = a * 0 + a * 0 : by rewrite left_distrib, show a * 0 = 0, by rewrite -(add.left_cancel H)

Structures (additional instances)

structure ring [class] (A : Type) extends add_comm_group A, monoid A, distrib A variable {A : Type} theorem ring.mul_zero [s : ring A] (a : A) : a * 0 = 0 := ... theorem ring.zero_mul [s : ring A] (a : A) : 0 * a = 0 := ... definition ring.to_semiring [instance] [s : ring A] : semiring A := ⦃ semiring, s, mul_zero := ring.mul_zero, zero_mul := ring.zero_mul ⦄

Structures (concrete instances)

protected definition int.linear_ordered_comm_ring [instance] : algebra.linear_ordered_comm_ring int := ⦃algebra.linear_ordered_comm_ring, int.integral_domain, le := int.le, le_refl := int.le.refl, le_trans := int.le.trans, le_antisymm := int.le.antisymm, lt := int.lt, le_of_lt := int.le_of_lt, lt_irrefl := int.lt.irrefl, ... le_iff_lt_or_eq := int.le_iff_lt_or_eq, le_total := int.le.total, zero_ne_one := int.zero_ne_one, zero_lt_one := int.zero_lt_one, add_lt_add_left := int.add_lt_add_left⦄
  • Is int a add_group? Yes
int.linear_ordered_comm_ring : algebra.linear_ordered_comm_ring int linear_ordered_comm_ring int → comm_ring int comm_ring int → ring int ring int → add_comm_group int add_comm_group int → add_group int

Quotients

  • Let A be any type, and let R be an equivalence relation on A. It is mathematically common to form the "quotient" A / R, that is, the type of elements of A "modulo" R.
  • Set theoretically, one can view A / R as the set of equivalence classes of A modulo R.
  • If f : A → B is any function that respects the equivalence relation in the sense that for every x y : A, R x y implies f x = f y, then f "lifts" to a function f' : A / R → B defined on each equivalence class [x] by f' [x] = f x.
structure setoid [class] (A : Type) := (r : A → A → Prop) (iseqv : equivalence r)

Quotients

The quotient package consists of the following constructors:

open setoid constant quot.{l} : Π {A : Type.{l}}, setoid A → Type.{l} namespace quot -- constructor constant mk : Π {A : Type} [s : setoid A], A → quot s notation `⟦`:max a `⟧`:0 := mk a -- recursors/eliminators constant lift : Π {A B : Type} [s : setoid A] (f : A → B), (∀ a b, a ≈ b → f a = f b) → quot s → B constant ind : ∀ {A : Type} [s : setoid A] {B : quot s → Prop}, (∀ a, B ⟦a⟧) → ∀ q, B q -- equality axiom constant sound : Π {A : Type} [s : setoid A] {a b : A}, a ≈ b → ⟦a⟧ = ⟦b⟧ end quot

Quotients

  • Quotients are used to prove function extensionality
  • They are used to define finite sets and bags in the standard library

Sylow theorem

variables {A : Type} [ambA : group A] [finA : fintype A] [deceqA : decidable_eq A] include ambA deceqA finA theorem cauchy_theorem : ∀ p, prime p → p ∣ card(A) → ∃ g : A, order(g) = p theorem first_sylow_theorem : ∀ p, prime p → ∀ n, p^n ∣ card(A) → ∃ (H : finset A) (sg : is_finsubg H), card(H) = p^n

Bundled structures

structure Semigroup : Type := (carrier : Type) (mul : carrier → carrier → carrier) (infix * := mul) (mul_assoc : ∀ a b c : carrier, (a * b) * c = a * (b * c)) notation a `*` b := Semigroup.mul _ a b attribute Semigroup.carrier [coercion] structure morphism (S1 S2 : Semigroup) : Type := (mor : S1 → S2) (resp_mul : ∀ a b : S1, mor (a * b) = (mor a) * (mor b)) attribute morphism.mor [coercion] example (S1 S2 : Semigroup) (f : morphism S1 S2) (a : S1) : f (a * a * a) = f a * f a * f a := calc f (a * a * a) = f (a * a) * f a : morphism.resp_mul f ... = f a * f a * f a : morphism.resp_mul f

Category Theory

theorem yoneda_embedding (C : Precategory) : C ⇒ set ^c Cᵒᵖ theorem contravariant_yoneda_embedding (C : Precategory) : Cᵒᵖ ⇒ set ^c C

Lua interface

  • Lua is an efficient embedded programming language
  • It is very popular in the computer gaming industry
  • Lean provides a Lua API
  • We can access terms, create definitions and tactics, type check terms etc
  • Lua scripts can be embedded in Lean files
  • examples/lua.lean

Javascript

  • Lean has been compiled as a Javascript library
  • We have used this library to implement the interactive tutorial
  • We can use it to write other applications (e.g., a fancier web IDE)
  • examples/ex.html

Future work

  • Auto tactic based on equational reasoning, matching, heuristic instantiation, …
  • Decision procedures for arithmetic
  • Efficient evaluator
  • Better support for proof by reflection
  • Better libraries (ongoing work)
  • Machine learning

Thank you